Trójkąty i takie tam69 K#62;G#62;: Bok trójkąta równobocznego ABC ma dł. 6 cm. Odcinki AE i BF są wysokościami tego trójkąta ,a S jest punktem przecięcia tych wysokości. Wykaż, że trókąty ASF i BSE są przystające. Oblicz miary kątów trójkąta ASF i długość jego boków. Nie wiem jak obliczyć te długość boków ? Pomożecie ?

K#62;G#62;: ?

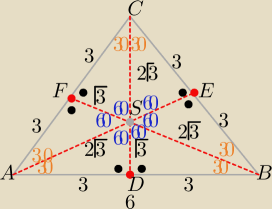
marika: |AB|=a=6

	a√3
h=|AE|=|BF|=|CD|=		= 3√3
	2

	2
|AS|=|BS|=CS|=		h= 2√3
	3

	1
|SE|=SF|=SD|=		h= √3
	3

ΔASF i ΔBSE są przystające z cechy (bbb)

K#62;G#62;: dziękuje

K#62;G#62;: Czemu tam jest 2/3h ? Skąd to wychodzi ?

5-latek: Punkt przeciecia sie w 3 wysokosci w trojkacie rownobocznym w jakin stosunku dzieli wysokosc ?

K#62;G#62;: to że to się przecina w 2/3h wyskości to jakaś własność mama rozumieć ?

K#62;G#62;: mam*

5-latek: tak ale 2/3h liczac od wierzcholka

K#62;G#62;: ok taka informacja mi umknęła dlatego nie umiałem rozwiązać

5-latek: https://matematykaszkolna.pl/strona/856.html a tu masz potwierdzenie tego faktu

K#62;G#62;: wiem

K#62;G#62;: A mam pytanie barycentrum trójkąta to ta własność ? Czy to coś innego ?

5-latek: nie to nie ta wlasnosc . Barycentrum to punkt przeciecia sie srodkowych w trojkacie

K#62;G#62;: Dobra mniejsza z tym ale i tak dzięki za pomoc

5-latek: Chociaz akuratnie w trojkacie rownobocznym to bedzie to samo dlatego ze w trojkacie rownoboczmym wysokosc opuszcona z wierzcholka trojkata jest jednoczesnie dwusieczna kąta i srodkowa . Ale w dowolnym trojkacie to nie

K#62;G#62;: Czyli aż taką wielką gafę nie walnąłem

5-latek: )