geometria analityczna Agnieszka: Punkty K=(0;1) L=(3;5) M=(0;5) są środkami boków trójkąta ABC. Wyznacz współrzędne wierzchołków trójkąta ABC

daras: https://matematykaszkolna.pl/strona/1750.html

Agnieszka: wzory znam, ale nie wiem jak rozwiązać

bezendu: x_a+x_c=0 x_a+x_b=6 x_c+x_b=0 y_a+y_c=2 y_a+y_b=10 y_b+y_c=10 Rozwiąż takie układy

daras: tak jak w 5 klasie podstawówki, chyba jesteś starsza ?

Agnieszka: Dzięki

Agnieszka: Bezendu pomogłeś bardzo. Daras, w szkole podstawowej nie ma układów równań, a tym bardziej z trzema niewiadomymi. Pozdrawiam

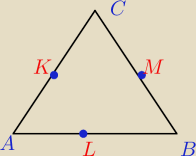
pigor: ..., lub np. niech K=(0,1) , L=(3,5) , M=(0,5) − środki boków Δ takie, że K=(0,1) − środek boku AC∥ML^→=[3,0] ⇒ 0(x−0)−3(y−1)=0 ⇔ y=1 − równanie AC; L=(3,5) − środek boku AB∥KM^→=[0,4] ⇒ 4(x−3)−0(y−5)=0 ⇔ x=3 − równanie AB; M=(0,5)− środek boku BC∥KL →=[3,4] ⇒ 4(x−0)−3(y−5)=0 ⇔ 4x−3y+15=0 −... BC, zatem z układów równań boków ΔABC, czyli prostych : AB i AC ⇒ x=3 i y=1 ⇒ mamy wierzchołek A=(3,1) , AB i BC ⇒ x=3 i 12−3y+15=0 ⇔ x=3 i y=9 ⇒ wierzchołek B=(3,9) , AC i BC ⇒ y=1 i 4x−3+15=0 ⇔ y=1 i x= −3 ⇒ wierzchołek C=(−3,1) . ...

Agnieszka: dzięki baaaardzo

daras: ale były toć to 3x to samo równanie wiec w czym problem? w takim razie zdradź nam co takiego studiujesz