geometria analityczna omamo: Dane są punkty A(−7, −3) B (5,3) i C ( 1,5) −NAPISZ RÓWNANIE OKRĘGU O ŚREDNICY AB)

5-latek: https://matematykaszkolna.pl/forum/253228.html

sushi_ gg6397228: i gdzie lezy punkt C ?

J: Takich okręgów jest nieskończenie wiele...

	1
Wybierz dowolny , o dowolnym środku i promieniu		IABI
	2

omamo: dzięks

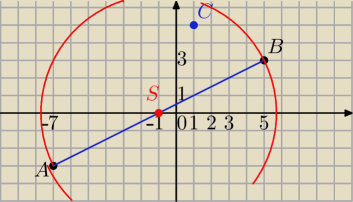
Mila: A(−7, −3) B (5,3) i C ( 1,5)

	−7+5		−3+3
S=		,		)=(−1,0) środek okręgu
	2		2

r=|SB|=√6²+3²=√36+9=√45=3√5 (x+1)²+y²=45

5-latek: Dobry wieczor Milu To teraz zobacz co napisala Mila i co ja napisalem w poprzednim poscie (nalezalo znac odpowiednie wzory

Mila: 2) Symetralna AB: Symetralna odcinak AB to zbiór wszystkich punktów jednakowo odległych od końców odcinka AB P(x,y) − dowolny punkt symetralnej AB |AP|=|BP| √(x+7)²+(y+3)²=√x−5)²+(y−3)² /² (x+7)²+(y+3)²=(x−5)²+(y−3)² x²+14x+49+y²+6y+9=x²−10x+25+y²−6y+9⇔ 14x+49+6y=−10x+25−6y 24x+24=−12y y=−2x−2 symetralna AB ================

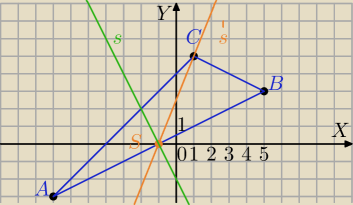
Mila: 2) symetralna AB: s: y=−2x−2 ============= 3) napisz równanie środkowej CS C=(1,5) S=(−1,0) prosta CS: y=ax+b 5=1a+b 0=−a+b dodaję stronami 2b=5 b=U{5}[2}

	5
a=
	2

	5		5
y=		x+		równanie prostej zawierającej środkową CS, S∊AB
	2		2

=============================================

Lukas: A równanie okręgu a) opisanaego na trójkącie o jakiś tam punktach b) wpisanego w trójkąt ?

omamo: Mila a skąd ta 6 i 3?:< (równanie okregu)

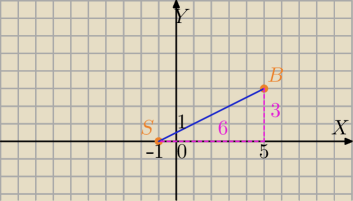
Mila: S=(−1,0) B=(5,3) Metoda geometryczna. Liczysz długość odcinka SB z tw. Pitagorasa, popatrz na rysunek, SB jest przeciwprostokątną. Albo z definicji długości odcinka w układzie wsp. SB|=√(5−(−1))²+(3−0)²=√6²+3² =√45

omamo: Mila jak by co to już wiem z wzoru na odleśłośc dwoch pkt od siebie dzienaD

Mila: To dobrze, ale w takim razie powinnaś wiedziec skąd ta 6 i 3.

omamo: taaak juz to mam