trygonometria (Znajdz dł. boków trójkata ABC...)

trygonometria (Znajdz dł. boków trójkata ABC...) plokm: kombinuje ale mi nie wychodzi Znajdz dł. boków trójkata ABC wiedządz że R=5/7 ,γ=120(stopni),α=30(stopni)

4 cze 18:41

PW: To ja tak całe życie, i ciągle nie starcza do pierwszego. Zagadkowo sformułowałeś treść zadania, jeżeli jednak R oznacza promień okręgu opisanego na trójkącie, to trzeba zastosować twierdzenie sinusów.

4 cze 18:45

plokm: no tak właśnie próbowałem i wychodzą mi 3 takie same boki chodź 1 kąt ma 120

4 cze 18:49

elf:

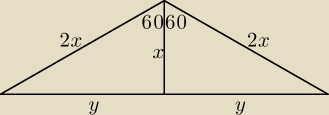
y = x√3

2x * 2x * 2x√3

Pole trójkąta P = x√3 * x = 

 5 
      4 * 
 7 

oblicz x

4 cze 18:51

AS: Z tw.sinusów

2x
	= 2R => x = Rsin(30^o)
sin(30^o)

4 cze 18:57

plokm: 1.skąd wiesz że bok to 2x 2.i boki są równe

4 cze 18:58

elf: powiedzieli mi w drugiej klasie gimnazjum

4 cze 19:00

elf: 2280

4 cze 19:04

Qmi:

A nie mozna od razu skorzystać z twierdzenia sinusów?

a
	= 2R
sinα

4 cze 19:12

plokm: tak właśnie zrobiłem ale mi wyszły 3 takie same boki

4 cze 19:16

Qmi:

	20
a, b mi wyszło
	7

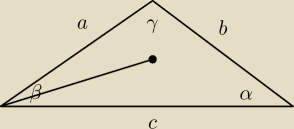
	√3
sin 120^o = (1*90^o + 30^o) = cos 30^o =
	2

c
	= 2R
sin γ

c		10
	=
sin γ		7

c

10

√3

=

 / *{

}

√3 
2 

7

2

	10		√3
c=		*{		}
	7		2

	10√3
c =
	14

tak mi wyszło

4 cze 19:31

plokm: nie możliwe żeby a,b było wieksze od c(też tak mi wyszło c) a,b u mnie =10/49

4 cze 20:09

Qmi:

	20
a,b mi wyszło		, ale racja, przeciwprostokątna jest krótsza od przyprostokątnych. lipton
	7

Dziubson. Nie umiemy.

4 cze 20:14

Bogdan: Jeśli trójkąt jest rozwartokątny, to środek okręgu opisanego leży poza trójkątem

4 cze 20:18

Qmi: Czyli twierdzenie sinusów tylko dla trójkątów ostrokątnych.

4 cze 20:24

Qmi: Zapewne elf zrobił dobrze i trzeba iść jego sposobem.

4 cze 20:24

Bogdan: rysunek

4 cze 20:24

Bogdan: Twierdzenie sinusów jest dla wszystkich trójkątów

4 cze 20:25

Qmi: Pierwszy raz widzę coś takiego, w sumie łatwy sposób, ale co jeśli tam nie ma kąta 120^o wtedy już nie ma takiego rysunku, tak?

4 cze 20:41

plokm: z tego co napisał bogdan (i narysował) dobrze mi wyszło

4 cze 20:42

Qmi: Innego wyjścia nie było, ale tym sposobem tego nie robiliśmy

4 cze 20:51

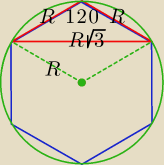
Bogdan: Wykorzystujemy w rozwiązaniu dane podane w zadaniu. Tu podany jest trójkąt równoramienny rozwartokątny, którego kąt rozwarty ma miarę 120^o − grzechem byłoby nie skorzystać z tych danych i skojarzyć ten trójkąt z sześciokątem foremnym.

4 cze 20:55

plokm: tylko że qmi ja zrobiłem z tw. sin i mi dobrze wyszło

4 cze 20:58