zadanie maturalne Adam :): W trójkącie jeden z kątów ma miarę 120 stopni. Dlugosci bokow tego trojkata sa kolejnymi wyrazami ciagu arytmetycznego, ktorego suma wynosi 30. Wyznacz stosunek dlugosci promienia okregu opisanego na tym trojkacie do dlugosci promienia wpisanego w ten trojkat.

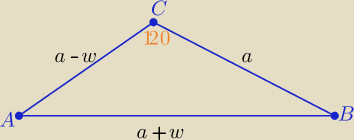
Eta: w−− różnica ciągu arytmetycznego , w<a Ob=a+w+a+a−w=30⇒ a= 10 |AB|=10+w , |AC|=10−w , |BC|= 10 z tw. kosinusów

	1
(10+w)2= 102+(10−w)2−2*10*(10−w)*cos120o , cos120o= −cos60o=−
	2

20w=100−20w+100−10w ⇒50w=200 ⇒ w=4 to boki trójkąta mają długości: 6, 10, 14

	14		14√3
z tw. sinusów :		=2R ⇒ R=
	sin120o		3

	1
P=		*10*6*sin120o =......... = 15√3
	2

	Ob		P
P=r*p , p=		= 15 to r=		=........ = √3
	2		p

R		14
	= ...... =
r		3

Eta: https://matematykaszkolna.pl/forum/7992.html Tak rozwiązałam 5 lat temu ( byłam jeszcze w podstawówce]]