Najmniejsza i największa wartość funkcji.
Radek: Najmniejsza i największa wartość funkcji.
f(x)=x4+4x3+6
Obliczam pochodną
f'(x)=4x3+12x2=4x2(x+3) I co dalej ?
Dziękuje
2 cze 22:38
zawodus: Warunek konieczny...
potem wystarczający....
2 cze 22:39
Radek: Hmyy w sumie ciężko mi powiedzieć bo dopiero zaczynam przygodę z tym.
2 cze 22:40
zawodus: To trzeba poczytać najpierw teorię
2 cze 22:44
Radek: Szukam jej właśnie
2 cze 22:45
2 cze 22:51
Radek: Hmyy czyli x=0 i x=−3
2 cze 22:52
zawodus: to są punkty podejrzane o ekstremum. Teraz badasz zachowanie pochodnej w otoczeniu tych
wartości.
2 cze 22:55
Radek: Hmyy a jak to zbadać ?
2 cze 22:57
Radek:
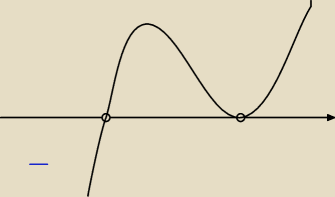
Nie wysatrczy szkic wykresu f'(x) i odczytać że f'(x)>0 ⇔ x należy (3,+
∞)
f'(x)<0 ⇔ x należy (−
∞−3)
2 cze 23:05
zawodus: Tak określamy monotoniczność. Po drugie to nie jest do końca ok.
2 cze 23:07
Saizou : a czy ta funkcja ma wartość największą ?
2 cze 23:08
zawodus: Oczywiście, że nie. Ja mówię o ekstremach lokalnych
2 cze 23:09
Radek: Zapomniałem dodać że mamy obliczyć w przedziale <−2,1>. To jeżeli od 3 rośnie to dla x=−2
osiągamin, a dla x=1 maks ?
2 cze 23:09
zawodus: Funkcja rośnie dla x ∊ (−3,0) zatem także w przedziale <−2,1>.
Zatem w −2 min, a w 1 max
2 cze 23:15
Radek: Czemu od (−3,0) rośnie a nie do +∞?
2 cze 23:20
Radek: To co się z nią dzieje od (0,+∞)?
2 cze 23:22
zawodus: To nas nie interesuje
2 cze 23:33
zawodus: Czekaj
W 0 mamy minimum lokalne i jeszcze liczysz wartość w 1 i wybierasz najmniejszą i największą
2 cze 23:34
Radek: −3 to maksimum a 0 to minimum ?
2 cze 23:43
zawodus: Nie , bo −3 nie należy do przedziału omawianego.
2 cze 23:46
Radek: To min dla x=−2 a maks dla x=1
2 cze 23:50