Rownania metoda graficzna.
Daniel: hej, pomoglby mi ktos zrobic te 2 podpunkty?

Rozwiaz rownania metoda graficzna i wykres
jakby ktos mogl narysowac

b)3x+y=−4
x−2y=−6
c) 2x−y=−1
x−2y=−5
1 cze 09:57
sushi_ gg6397228:
nie umiesz narysować prostej ?
1 cze 10:02
Daniel: Nie za bardzo... Choc jakbys zrobil podpunkt b) to moze bym sobie poradzil z podpunktem c)
1 cze 10:04
sushi_ gg6397228:
a tabelkę umiesz zrobisz ?
1 cze 10:08
Daniel: Ale nie trzeba tabelki, prawda?
1 cze 10:11
sushi_ gg6397228:
trzeba zrobic tabelke, naniesc punkty i zrobić "kreske"− prostą, przechodzącą przez te punkty
1 cze 10:12
Daniel: A zrobilbys podpunkt b? Mialbym troche obraz tego jak zrobic podpunkt c)

1 cze 10:15
Saizou :
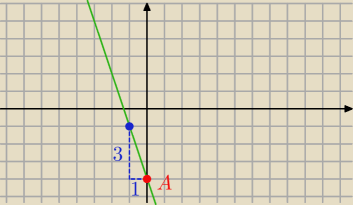
ja zawsze robiłem tak np.
3x+y=−4
y=−3x−4
zaznaczałem punkt (0:b) w tym przypadku A=(0:−4), i wyznaczałem kąt nachylenia, czyli tgα=a,
gdzie a to współczynnik kierunkowy
1 cze 10:17
sushi_ gg6397228:
przyklady są zrobione w pedręczniku lub poszukac na stronie, a nie na gotowca czekac
kazde rownanie trzeba doprowadzic to postaci
y= a*x + b
tabelka np:
x: 1 2 3 4
y: .... ... ... ...
potem naniesc punkty do układu i poprowadzić prostą przechodzącą przez te punkty
1 cze 10:18
1 cze 10:20
Saizou :
ale rozbudowana ta tabelka

nie lepiej wyznaczyć tylko 2 punkty

1 cze 10:22
Daniel: Dalej nie rozumiem, Saizou mozesz powoli wytlumaczyc?
1 cze 10:24
Saizou :
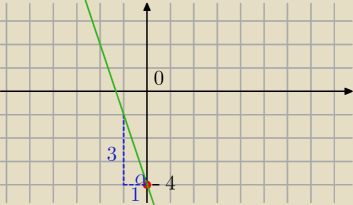
do narysowania prostej potrzebne są min. 2 punkty, warto wiedzieć że punkt przecięcia z osią Y
ma współrzędne (0:b), dla prostej w postaci y=ax+b oraz że współczynnik kierunkowy a to
tangens nachylenia prostej do osi X tgα=a
np. y=−3x−4
− punkt przecięcia z osią Y to (0:−4), bo f(0)=−4
− tgα=−3 (minus wskazuje na to że będzie to funkcja malejąca), i teraz z definicji tangensa
dla kąta prostego (tg to stosunek przyprostokątnej na przeciw kąta α do przy prostokątnej przy
kącie alfa)
1 cze 10:33
Daniel: I to jest juz caly podpunkt b zrobiony?
1 cze 10:42
Daniel: Ale ten podpunkt b) (rownanie) trzeba rozwiazac, tak? Mi wyszlo cos takiego a)
−3x+y=−5
x+y=1 |−x
y=1−x
−3x+1−x=−5 |−1
y=1−x
−4x=−6 |:(−4)
x=1,5
y=1−1,5=−0,5
b)
3x+y=−4
x−2y=−6 |+2y
x=−6+2y
−18+6y−2y=−6 |+18
x=−6+2y
4y=12 |:4
y=3
x=−6−2*3=−6−6=−12
1 cze 10:46
Saizou : to jest jedna prosta, teraz trzeba narysować na tym samym rysunku drugą
| | 1 | |
x−2y=−6 ⇒−2y=−x−6⇒y= |
| +3 |
| | 2 | |
1 cze 10:47
Daniel: tfu, pomylilem przyklady
b)
3x+y=−4
x−2y=−6 |+2y
x=−6+2y
−18+6y−2y=−6 |+18
x=−6+2y
4y=12 |:4
y=3
x=−6−2*3=−6−6=−12
1 cze 10:47
Hajtowy: Wczoraj tłumaczyłem jak rysować...

1 cze 10:48
Saizou :
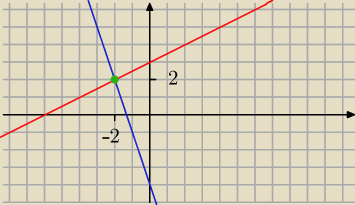
x=−2 y=2
1 cze 10:50
Daniel: Kurde nie rozumiem.... Czy to jest dobrze zrobione
b)
3x+y=−4
x−2y=−6 |+2y
x=−6+2y
−18+6y−2y=−6 |+18
x=−6+2y
4y=12 |:4
y=3
x=−6−2*3=−6−6=−12
1 cze 10:52
Saizou :
3x+y=−4 /*2
x−2y=−6
6x+2y=−8
x−2y=−6
=======+
7x=−14
x=−2
−2−2y=−6
−2y=−4
y=2
1 cze 10:54
Saizou :
tu masz błąd
−18+6y−2y=−6 |+18
1 cze 10:56
Daniel: Czyli c) tez jest zle zrobiony?
c)
2x−y=−1
x−2y=−5 |+2y
x=−5+2y
−10+4y−y=−1 |+10
x=−5+2y
3y=9 |:3
y=3
x=−5+2*3=−5+6=1
1 cze 10:57
Saizou : ten jest ok
1 cze 10:59
Daniel: Czyli teraz zaznaczyc na wykresie y=3 a x=1 ? Pomoglbys jeszcze raz?

1 cze 11:00
Saizou :
nie, jeśli chcesz rozwiązać graficznie to rysujesz wyjściowe proste, czyli
2x−y=−1
x−2y=−5
1 cze 11:02
Daniel: hmm, wiec te rozwiazane rownania to jaka metoda sa

1 cze 11:03
Saizou :
to że liczysz.... to metoda algebraiczna
1 cze 11:05
Daniel: Ty tez cos tu liczyles
3x+y=−4 /*2
x−2y=−6
6x+2y=−8
x−2y=−6
=======+
7x=−14
x=−2
−2−2y=−6
−2y=−4
y=2
1 cze 11:08
Saizou :
no to co przeliczyłem bo chciałem sprawdzić czy nie ma błędu

1 cze 11:11
Daniel: Czyli w metodzie graficznej nie ma tak naprawde co liczyc?
1 cze 11:12
Saizou :

dokładnie, ew. jak 'liczysz' tabelkę to możesz sobie policzyć xd
tabelka polega na tym że wybierasz sobie dowolne x−y dziedziny i obliczasz dla nich wartości,
potem zaznaczasz te punkty w układzie i rysujesz prostą
1 cze 11:15
Daniel: a zrobilbys jeszcze podpunkt c)? Moze cos wiecej bede rozumial

bo juz mi cos trybi
1 cze 11:19
Hajtowy: Saizou nie rób... Wczoraj to samo pisał... czyli chce gotowca.
0 nauki, 100% lenistwa.
1 cze 11:19
Saizou : to jak trybi to zrób sam

1 cze 11:23
Daniel: Dobra... zrobie sam a Wy ocenicie
c) 2x−y=−1 => y=2x−1
x−2y=−5 => y=5−x
2x−1=5−x
3x=6 | :3
x=2
tak?
1 cze 11:25
nissan 2.0.TD: A co to jest x=2?
1 cze 11:26
Hajtowy:
c)
2x−y=−1 ⇒ y=2x+1
4x+2 = x + 10
3x = 8
1 cze 11:27
Daniel: Miejsce zerowe? czyli tam gdzie sie przetnie prosta z x
1 cze 11:28
Daniel: Myslalem, ze juz to powoli rozumie, ale tym to mnie dobiles

1 cze 11:30
nissan 2.0.TD: czyli x zle policzyles . Ale tez to nie jest miejsce zerowe . Poczytaj sobie co to jest
| | 8 | |
miejsce zwerowe funkcji . Przeciez porownales dwie proste . czyli x= |
| to jest |
| | 3 | |
wspolrzedna x
owa punktu przeciecia sie tych prostych . Teraz podstaw te wyliczone x do np
1 ronania prostej i wylicz wspolrzedna y
kowa punktu przeciecia tych prostych .
Teraz narysysuj te prodte w ukladzie i sprawdez czy dobrze wyliczyles punkt przeciecia
1 cze 11:33
Daniel: z ulamkami sobie nie poradze xD
1 cze 11:39
nissan 2.0.TD: To sie cofnij do podstawoki i naucz sie ulamkow .
1 cze 11:40
Hajtowy: nissan 2.0 TDI 
Daniel sobie chyba jaja robi albo po prostu czeka na gotowca bo nic nie rozumie...
1 cze 11:42
nissan 2.0.TD: Hajtowy tylko jednak 2.0TD ( bez I)

1 cze 11:45
nissan 2.0.TD: Chyba jednak nie umie

1 cze 11:46
Hajtowy:
Pytanie co robi na lekcjach

Dla niektórych matma jest "koszmarem" i nie chcą się jej uczyć.
Drudzy mogą powiedzieć, że się uczą ale nie rozumieją.
Trzeci powie, że próbuje ale nie wychodzi.
A dla czwartego będzie wszystko łatwe

Byłem w rozszerzonej klasie, byłem jednym z najgorszych ale dałem rade

1 cze 11:49
Daniel: Nom...
1 cze 11:50
Daniel: Hajtowy, jakbys byla na naszej lekcji z babka co mamy to bys sie nie dziwil

1 cze 11:51
Daniel: byl*
1 cze 11:51
krystek: Czego nie rozumiesz, zapisz postaram się wyjaśnić Tobie.
1 cze 11:56
Daniel: jak zrobic podpunkt c)... bez nerwow

1 cze 12:05
krystek: 1)Wyznaczasz y z pierwszego i drugiego równania . Zrób to, poprawię.
1 cze 12:07
Hajtowy: Nikt się nie denerwuje
 krystek
krystek już Ci pomoże i spróbuje wytłumaczyć
Ja próbowałem ale mi nie wyszło

1 cze 12:14
Daniel: c) 2x−y=−1 => y=2x+1
1 cze 12:14
krystek: drugie źle
| | 1 | | 5 | |
y= |
| x+ |
| dzielisz każdy wyraz przez 2 |
| | 2 | | 2 | |
teraz naszkicuj wykres ( wyznacz do każdego równania dwa punkty przez które przejdzie wykres−
tabela)
1 cze 12:18
krystek: | | −1 | |
y=2x+1 x=0 to y=1 x= |
| to y=0 i już masz dwa punkty |
| | 2 | |
1 cze 12:21
krystek:
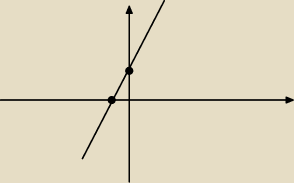
1 cze 12:25
Daniel: kurde nie rozumiem.. dobra poddaje sie

1 cze 12:26
krystek: Analogicznie nakreś ldrugą prostą i współrzędne punktu przecięcia prostych są rozwiązaniem
układu
1 cze 12:27
krystek: Czego nie rozumiesz?
1 cze 12:27
krystek: x=0 to y=2*0+1=1
1 cze 12:28
Daniel: y=2x+1 x=0 to y=1
obliczyles to w pamieci czy jak?
1 cze 12:28
krystek: | | −1 | | −1 | |
x= |
| to y=2* |
| +1=−1+1=0 |
| | 2 | | 2 | |
1 cze 12:30
mix:
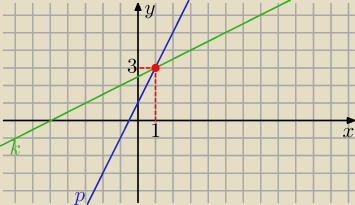 p
p : y=2x+1
p ∩
k=
(1,3)
1 cze 12:30
Daniel: ale z tego co widze to naszkicowales x=1 i y=2 z tych kropek tak wynika
1 cze 12:31
Daniel: ale z tego co widze to naszkicowales x=1 i y=2 z tych kropek tak wynika
1 cze 12:31
Daniel: ale z tego co widze to naszkicowales x=1 i y=2 z tych kropek tak wynika
1 cze 12:31
krystek: Wybierasz dowolne x i obliczasz y
np x=2 to y=2*2+1=4+1=5
1 cze 12:31
Hajtowy: Te kropki są dla Twojej wiadomości, żebyś zauważył że jest to pkt A=(1;3)
1 cze 12:32
krystek: Współrzędne punktu to (x,y)
| | −1 | |
Jeden punkt (0, 1) drugi to ( |
| ,0) |
| | 2 | |
1 cze 12:34
krystek: Hajtowy nie mieszaj jemu , Rozwiązaniem są współrzędne punktu (1,3)
1 cze 12:35
Daniel: Dobra wszystko mi sie miesza... czyli rozwiazanie to (1,3) ?
1 cze 12:37
krystek: Tak, poukładaj sobie wszystko na spokojnie . Popatrz w zeszyt jak kreśliliście funkcję liniową
np y=3x+5 czy układaliście tabelkę czy przesuwaliście y=3x o wektor [0,5] lub w pamięci
liczyliście( bez tabeli)
1 cze 12:40
Daniel: Okej

1 cze 12:43
krystek: Wieczorem będe ,pytaj aż zrozumiesz!
1 cze 12:45
 Rozwiaz rownania metoda graficzna i wykres
jakby ktos mogl narysowac
Rozwiaz rownania metoda graficzna i wykres
jakby ktos mogl narysowac  b)3x+y=−4
x−2y=−6
c) 2x−y=−1
x−2y=−5
b)3x+y=−4
x−2y=−6
c) 2x−y=−1
x−2y=−5

 ja zawsze robiłem tak np.
3x+y=−4
y=−3x−4
zaznaczałem punkt (0:b) w tym przypadku A=(0:−4), i wyznaczałem kąt nachylenia, czyli tgα=a,
gdzie a to współczynnik kierunkowy
ja zawsze robiłem tak np.
3x+y=−4
y=−3x−4
zaznaczałem punkt (0:b) w tym przypadku A=(0:−4), i wyznaczałem kąt nachylenia, czyli tgα=a,
gdzie a to współczynnik kierunkowy
 nie lepiej wyznaczyć tylko 2 punkty
nie lepiej wyznaczyć tylko 2 punkty 
 do narysowania prostej potrzebne są min. 2 punkty, warto wiedzieć że punkt przecięcia z osią Y
ma współrzędne (0:b), dla prostej w postaci y=ax+b oraz że współczynnik kierunkowy a to
tangens nachylenia prostej do osi X tgα=a
np. y=−3x−4
− punkt przecięcia z osią Y to (0:−4), bo f(0)=−4
− tgα=−3 (minus wskazuje na to że będzie to funkcja malejąca), i teraz z definicji tangensa
dla kąta prostego (tg to stosunek przyprostokątnej na przeciw kąta α do przy prostokątnej przy
kącie alfa)
do narysowania prostej potrzebne są min. 2 punkty, warto wiedzieć że punkt przecięcia z osią Y
ma współrzędne (0:b), dla prostej w postaci y=ax+b oraz że współczynnik kierunkowy a to
tangens nachylenia prostej do osi X tgα=a
np. y=−3x−4
− punkt przecięcia z osią Y to (0:−4), bo f(0)=−4
− tgα=−3 (minus wskazuje na to że będzie to funkcja malejąca), i teraz z definicji tangensa
dla kąta prostego (tg to stosunek przyprostokątnej na przeciw kąta α do przy prostokątnej przy
kącie alfa)

 x=−2 y=2
x=−2 y=2



 dokładnie, ew. jak 'liczysz' tabelkę to możesz sobie policzyć xd
tabelka polega na tym że wybierasz sobie dowolne x−y dziedziny i obliczasz dla nich wartości,
potem zaznaczasz te punkty w układzie i rysujesz prostą
dokładnie, ew. jak 'liczysz' tabelkę to możesz sobie policzyć xd
tabelka polega na tym że wybierasz sobie dowolne x−y dziedziny i obliczasz dla nich wartości,
potem zaznaczasz te punkty w układzie i rysujesz prostą
 bo juz mi cos trybi
bo juz mi cos trybi


 Daniel sobie chyba jaja robi albo po prostu czeka na gotowca bo nic nie rozumie...
Daniel sobie chyba jaja robi albo po prostu czeka na gotowca bo nic nie rozumie...


 Dla niektórych matma jest "koszmarem" i nie chcą się jej uczyć.
Drudzy mogą powiedzieć, że się uczą ale nie rozumieją.
Trzeci powie, że próbuje ale nie wychodzi.
A dla czwartego będzie wszystko łatwe
Dla niektórych matma jest "koszmarem" i nie chcą się jej uczyć.
Drudzy mogą powiedzieć, że się uczą ale nie rozumieją.
Trzeci powie, że próbuje ale nie wychodzi.
A dla czwartego będzie wszystko łatwe  Byłem w rozszerzonej klasie, byłem jednym z najgorszych ale dałem rade
Byłem w rozszerzonej klasie, byłem jednym z najgorszych ale dałem rade 


 krystek już Ci pomoże i spróbuje wytłumaczyć
Ja próbowałem ale mi nie wyszło
krystek już Ci pomoże i spróbuje wytłumaczyć
Ja próbowałem ale mi nie wyszło 


 p : y=2x+1
p : y=2x+1
