f
Lukas:
Określ liczbę rozwiązań równania w zależności od prametru m.
|x2−6x+8|+|x2−6x+5|=m
x2−6x+8≥0
x∊(−∞,2>suma<4,∞)
x∊(2,4) malejąca
x2−6x+5≥0
x∊(−∞.1>suma<4,∞)
x∊(1,4)
I teraz jak dać te przedziały ?
31 maj 16:53
Krystian: 2015 matura? Czy już po maturze?
31 maj 16:54
Lukas:
Już po maturze.
31 maj 17:11
Lukas:
Ale tu nie chodzi o rozwiązanie tylko jak ustalić wzór funkcji w przedziale

31 maj 19:55
Eta:
Przede wszystkim wyznacz poprawnie ( masz błąd) miejsca zerowe
x2−6x+5
31 maj 20:01
Eta:
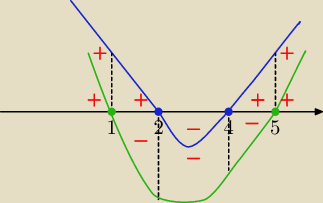
Wczoraj rozrysowywała Ci to
krystek (
1/
2/
3/
31 maj 20:06
Lukas:
x2−6x+5=0
x1=1 x2=5
wartości dodatnie
x∊(−∞,1>suma<5,∞)
x∊(1,5)
Ale nadal tego nie rozumiem.
31 maj 20:08
Mila:

zaznaczymy na osi.
f(x)=|x
2−6x+8|+|x
2−6x+5|
|x
2−6x+8|=x
2−6x+8 dla x
2−6x+8≥0⇔x≤2 ∪ x≥4
|x
2−6x+8|=−x
2+6x−8 dla x∊(2,4)
|x
2−6x+5|=x
2−6x+5 dla x
2−6x+5≥0⇔ x≤1 lub x≥5
|x
2−6x+5|=−x
2+6x−5 dla x∊(1,5)
(1) x≤1
f(x)=x
2−6x+8+x
2−6x+5⇔
f(x)=x
2−12x+13
(2)
(3)
(4)
(5)x≥5
f(x)=x
2−12x+13
Dalej napisz sam, potem będziemy szkicować wykres.
31 maj 20:53
Lukas:
Ja nic z tego zapisu nie rozumiem.

Chyba sobie odpuszczę tą naukę jednak.
31 maj 21:01
Piotr 10: |x2−6x+8|+|x2−6x+5| = m
Liczę miejsca zerowe ( m0 )
Ix2 −6x+8I=0
x2−6x+8=0
Δ=36 − 32 =4 √Δ=2
x1=4 v x2=2
Teraz rysujesz sobie oś liczbową zaznaczasz te miejsca zerowe i rysujesz parabolę ( nie ważne
jaki ma wierzcholek )
Z drugim robisz tak samo
Wpierw zrób to
31 maj 21:08
Piotr 10: I obydwa wykresy paraboli mają być na jednej osi liczbowej
31 maj 21:08
Lukas:
Ale w tym wątku nie chodzi o rozwiązanie graficzne tylko jak ustalać wzór funkcji w
przedziale....
31 maj 21:12
Piotr 10: A czy ja robię to graficznie

Zastanów się... Te wykresy mają być tylko szkicami i mają nam
wskazać znaki funkcji ( dodatnie lub ujemne). Już tyle osób Ci to tłumaczy, a Ty nadal swoje.
I trochę pokory kolego, bo jak przychodzi pomóc innym osobom to odsyłasz ich do jakiś stron
internetowych, np. wikipedia lub odsyłasz ich do teorii.
31 maj 21:16
Lukas:
A nie widziałeś linku w którym prosiłem o link ? Więc może zaznaj się z tematem a nie mnie
pouczasz...
31 maj 21:17
31 maj 21:23
Mila:
Lukas, rozumiesz definicję wartości bezwzględnej?
|x|=x dla x≥0
|x|=−x dla x<0
Zamiast pojedynczego x−a masz pod wartością bezwzględną wzór funkcji kwadratowej, i uogólniasz
.
|x2−6x+8|=x2−6x+8 dla x2−6x+8≥0⇔x≤2 ∪ x≥4
I wróć do mojego zapisu, zobacz co na osi zaznaczyłam, abyś w przedziałach mógł ustalic wzór
f(x).
31 maj 21:27
Lukas:
Rozumiem i wyznaczyłem przedziały.
31 maj 21:30
Lukas:
|2x+4|+|x+6|=5
Z takimi równaniami nie mam problemu a tę z wartością bez nie do przejścia.
31 maj 21:37
Mila:
Na osi masz zaznaczone jakie wyrażenia masz podstawić opuszczając |..|.
31 maj 21:42
Lukas:
Dziękuję za wytłumaczenia ale myślę, że i tak taki przykłady są za trudne jak dla mnie.
31 maj 21:45
Mila:
To jest z matury R.
31 maj 21:52
Lukas:
A ja pisałem P i trudno mi zrozumieć niektóre fakty, a dwa uczę się sam w domu.
31 maj 21:54
Piotr 10: Spokojnie, nie można poddawać się. Zajmij się innymi zadaniami, za miesiąc spróbujesz takie
zrobić.
31 maj 22:00
Lukas:
Tych prostych zrobiłem już dużo, teraz chce podnieś poprzeczkę.
31 maj 22:01
Lukas:
A dwa tutaj 20:53 nie są podane przedziały w jakich mam to rozpatrywać
(−
∞,1)
<1,2)
<2,4)
<4.5)
<5,,6)
I znowu tutaj mam sprzeczność

31 maj 22:30
kyrtap: Jak chcesz mogę Tobie pieprznąć(zeskanować) cały zeszyt z rozwiązaniami takich równań i
nierówności?
31 maj 23:41
Lukas:
Dzięki ale nie trzeba

1 cze 00:01
Mila:
Chciałam, abyś sam odczytał te przedziały, zawsze się oburzasz na gotowce więc tylko jeden
przypadek rozwiązałam.
Jaka sprzeczność?
Patrz na oś.
(−∞,1>∪(1,2>∪(2,4) ∪<4,5)∪<5,∞)
1 cze 17:06
Lukas:
Ale ja inaczej zapisałem przedziały. 22:30
1 cze 17:09
mix:

1 cze 17:13
Lukas:

1 cze 17:15
Mila:
Masz inne domknięcia, a przedział <5,6) to na jakiej podstawie? Skąd ta szóstka?
1 cze 17:21
Lukas:
Ta 6 to pomyłka zwyczajna
1 cze 17:24
Mila:
Dobrze. To jaka będzie postać f(x) w każdym z tych przedziałów?
1 cze 17:28
Lukas:
Za 10 minut postaram się napisać w każdym przedziale.
1 cze 17:33
Lukas:
1. (−∞,1)
f(x)=x2−6x+8+x2−6x=5
f(x)=2x2−12x+13
2, <1,2) tutaj mam sprzeczność
f(x)=x2−6x+8 i badając znak funkcji f(x)=|x2−6x+5| w przedziale <1,2)
dla 1 f(x)=x2−6x+5
ale dla 1,5 mam −1,75 i nie wiem czy opuścić ze zmianą znaków czy bez zmiany.
1 cze 17:50
Mila:
Lukasz patrzy na mój rysunek 20:53.
A w ogóle to jak badasz Twoim sposobem znak wyrażenia to bierz liczbę ze środka przedziału.
Jednak po to zaznaczyłam gdzie funkcje pod wartością |..| mają wartości dodatnie abyś nie
musiał tego robić, tylko odczytujesz z osi.
Nad przedziałem (1,2) jest niebieska linia i na niej x2−6x+8
Pod przedziałem nie ma zielonej linii⇔x2−6x+5 przyjmuje tam wartości ujemne, trzeba zmienic
znak
|x2−6x+5|=−x2+6x−5
Dla x∊(1,2>
f(x)=x2−6x+8−x2+6x−5=3
f(x)=3 funkcja stała.
Przedział (2,4)
Nie ma nad nim niebieskiej linii i nie ma zielonej ⇔obie funkcje pod |..| mają wartości ujemne⇔
f(x)=−x2+6x−8−x2+6x−5
f(x)=−2x2+12x−13
Dalej sam
1 cze 18:09
Lukas:
ale moje wytłumaczenie jest logiczne ?
1 cze 18:14
Mila:
Jeśli w przedziale wyrażenie jest ujemne to zmieniasz znak opuszczając wartość |..|.
Jeśli dla x=−1,5 otrzymałeś dla jednej funkcji (+) a dla drugiej (−), to pierwszą zostawiasz ,
a w drugiej zmieniasz znak.
1 cze 18:27
Lukas:
Wiem, że mam zmieniać znak albo zostawiać jeżeli jest dodatnie
ale dla drugiej części nie dla |x2−6x+8| bo do tego wychodzi dodatnie ale dla tego |x2−6x+5|
wychodzi, że ujemne i dodatnie.
1 cze 18:46
zawodus:
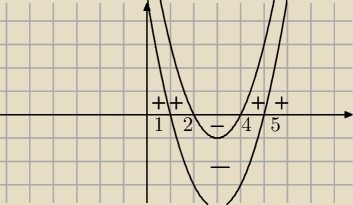
Ja zawsze robię w ten sposób.
Teraz widzę, w jakim przedziale, funkcje przyjmują jakie znaki

1 cze 19:20
Mila:
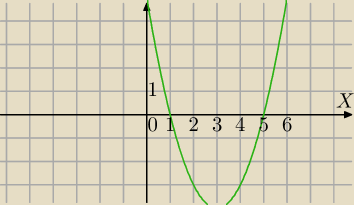 Bierzesz punkt ze środka przedziału
Bierzesz punkt ze środka przedziału.
g(x)=x
2−6x+5
g(1)=1−6+5=0
x
2−6x+5<0⇔
x∊(1,5)
To jakim cudem wychodzi Ci dodatnia w tym przedziale?
1 cze 19:23
Mila: ?
1 cze 19:25
Lukas:
Jakim cudem ?
Skoro mam drugi przedział
<1,2) x
2−6x+5
to dla f(1)=5
dla f(1,5)=−1,75
Bez sensu jest to ? Niezależnie jaki punkt z przedziału wezmę to powinno być albo ujemne
wartości na cały przedziale albo dodatnie a tak nie wiadomo czy to jest dodatnie czy może
ujemne

1 cze 19:37
Mila:
12−6*1+5=0 a nie 5
(1,5)2−6*1,5+5=2,25−4=−1,75
1 cze 19:56
Lukas:
No to potwierdza moją tezę, że ta funkcja nie w cały przedziela przyjmuję wartości ujemne ale
też i nie w cały dodatnie..
1 cze 20:12
Mila:
O jakiej funkcji mówisz?
1 cze 20:23
Lukas:
f(x)=|x2−6x+5| w przedziale <1,2)
1 cze 20:24
Mila:
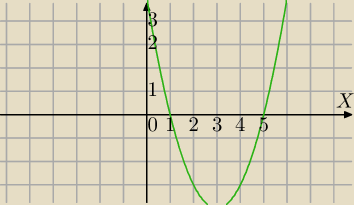
|x
2−6x+5|≥0 dla x∊R
g(x)=x
2−6x+5≥0 dla x≤1 lub x≥5
g(x)=x
2−6x+5<0 dla x∊(1,5)
Nie wiem dlaczego tego nie widzisz?
1 cze 20:29
Lukas:
Widzę to i teraz mając przedział <1,2) 0.... i w dół a zero nie powinno należeć do tego
przedziału.
Biorę się za inne zadania bo tę są za trudne dla mnie.
1 cze 20:44
Lukas:
W równaniach liniowych to zawsze jest spełnione
|x+2|+|x−3|=3 prosty przykład
1.(−
∞−2)
i na cały przedziale |x+2| przyjmuje wartości ujemne więc czemu z tymi kwadratowymi tak nie
jest

?
1 cze 23:26

 Wczoraj rozrysowywała Ci to krystek (
1/
2/
3/
Wczoraj rozrysowywała Ci to krystek (
1/
2/
3/
 zaznaczymy na osi.
f(x)=|x2−6x+8|+|x2−6x+5|
|x2−6x+8|=x2−6x+8 dla x2−6x+8≥0⇔x≤2 ∪ x≥4
|x2−6x+8|=−x2+6x−8 dla x∊(2,4)
|x2−6x+5|=x2−6x+5 dla x2−6x+5≥0⇔ x≤1 lub x≥5
|x2−6x+5|=−x2+6x−5 dla x∊(1,5)
(1) x≤1
f(x)=x2−6x+8+x2−6x+5⇔
f(x)=x2−12x+13
(2)
(3)
(4)
(5)x≥5
f(x)=x2−12x+13
Dalej napisz sam, potem będziemy szkicować wykres.
zaznaczymy na osi.
f(x)=|x2−6x+8|+|x2−6x+5|
|x2−6x+8|=x2−6x+8 dla x2−6x+8≥0⇔x≤2 ∪ x≥4
|x2−6x+8|=−x2+6x−8 dla x∊(2,4)
|x2−6x+5|=x2−6x+5 dla x2−6x+5≥0⇔ x≤1 lub x≥5
|x2−6x+5|=−x2+6x−5 dla x∊(1,5)
(1) x≤1
f(x)=x2−6x+8+x2−6x+5⇔
f(x)=x2−12x+13
(2)
(3)
(4)
(5)x≥5
f(x)=x2−12x+13
Dalej napisz sam, potem będziemy szkicować wykres.
 Chyba sobie odpuszczę tą naukę jednak.
Chyba sobie odpuszczę tą naukę jednak.
 Zastanów się... Te wykresy mają być tylko szkicami i mają nam
wskazać znaki funkcji ( dodatnie lub ujemne). Już tyle osób Ci to tłumaczy, a Ty nadal swoje.
I trochę pokory kolego, bo jak przychodzi pomóc innym osobom to odsyłasz ich do jakiś stron
internetowych, np. wikipedia lub odsyłasz ich do teorii.
Zastanów się... Te wykresy mają być tylko szkicami i mają nam
wskazać znaki funkcji ( dodatnie lub ujemne). Już tyle osób Ci to tłumaczy, a Ty nadal swoje.
I trochę pokory kolego, bo jak przychodzi pomóc innym osobom to odsyłasz ich do jakiś stron
internetowych, np. wikipedia lub odsyłasz ich do teorii.




 Ja zawsze robię w ten sposób.
Teraz widzę, w jakim przedziale, funkcje przyjmują jakie znaki
Ja zawsze robię w ten sposób.
Teraz widzę, w jakim przedziale, funkcje przyjmują jakie znaki 
 Bierzesz punkt ze środka przedziału.
g(x)=x2−6x+5
g(1)=1−6+5=0
x2−6x+5<0⇔
x∊(1,5)
To jakim cudem wychodzi Ci dodatnia w tym przedziale?
Bierzesz punkt ze środka przedziału.
g(x)=x2−6x+5
g(1)=1−6+5=0
x2−6x+5<0⇔
x∊(1,5)
To jakim cudem wychodzi Ci dodatnia w tym przedziale?

 |x2−6x+5|≥0 dla x∊R
g(x)=x2−6x+5≥0 dla x≤1 lub x≥5
g(x)=x2−6x+5<0 dla x∊(1,5)
Nie wiem dlaczego tego nie widzisz?
|x2−6x+5|≥0 dla x∊R
g(x)=x2−6x+5≥0 dla x≤1 lub x≥5
g(x)=x2−6x+5<0 dla x∊(1,5)
Nie wiem dlaczego tego nie widzisz?
 ?
?