logarytm
Lukas:
Określ znak liczby
logab a>1 b>1
znak + ?
29 maj 20:36
29 maj 20:38
Lukas:
Ale tu jest tylko donośnie a
29 maj 20:39
Eta:
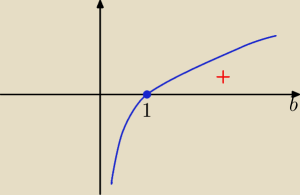
29 maj 20:41
Lukas:
ok dziękuję
29 maj 20:42
Lukas:
logab a∊(0,1) b∊(0,1)
− ?
29 maj 21:48
ZKS:
Niby dlaczego ujemne to ma być?
29 maj 21:51
Mila:
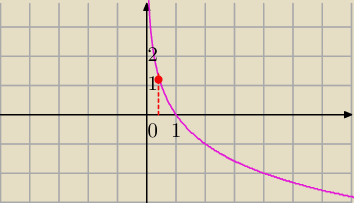
log{1/2)x −funkcja malejąca
(+) dla b∊(0,1)
29 maj 21:53
29 maj 21:53
Lukas:
Wyznacz wszystkie liczby spełniające nierówność
log2p<3
p∊(0,∞)
co dalej ? Proszę tylko o wskazówkę a nie gotowca.
29 maj 22:24
razor: 3 = log28
29 maj 22:25
Lukas:
log2p<log28
p<8
p∊(−∞,8)
ostatecznie
p∊(0,8) ?
29 maj 22:27
razor: tak
29 maj 22:27
Lukas:
Rozwiąż równanie logx2(x + 2) = 1 .
x2>0 i x2≠1
x∊R\{−1,0,1}
?
29 maj 22:54
Piotr:
a co to jest ? dziedzina ? a gdzie x+2 > 0 ?
29 maj 22:57
razor: jeszcze x+2 > 0 i dziedzina będzie ok
29 maj 22:57
ZKS:
Przydatny wzorek do logarytmów
29 maj 23:02
Piotr:
cos mi tu zniknelo
29 maj 23:03
Lukas:
x+2>0
x>−2
D=(−2,∞)\{0,1}
29 maj 23:05
razor: a co z −1?
29 maj 23:05
Piotr:
jakby byl szybki to by widzial odpowiedz
29 maj 23:06
Lukas:
Jeszcze −1 należy wyrzucić
Ale teraz mam problem
log
x2(x+2)=log
x2 ?
29 maj 23:09
Piotr:
z definicji rozwiaz.
29 maj 23:09
razor: logx2(x+2) = logx2(x2)
29 maj 23:09
Lukas:
x+2=x
2
x
2−x−2=0
Ok, już sobie poradzę
razor jesteś moim mentorem !
29 maj 23:11
Piotr:
dobra, juz sie nie odzywam.
29 maj 23:12
kyrtap: Piotr przykro mi jesteś najsłabszym ogniwem
29 maj 23:23
Lukas:
29 maj 23:24