gr bezendu: Korzystając z definicji granicy ciągu wykaż, że:

	3n2+2
limn→∞		=3
	n2+2n+1

Jak to zrobić ? Umiem policzyć granice ale to trzeba z tego |a_n−g|<ε ?

	3n2+2
|		−3|<ε
	n2+2n+1

Nie mam podanego epsiolna ?

bezendu:

	6n+1
|		|<ε ?
	n2+2n+1

jakubs: Tutaj chyba trzeba wyznaczyć n

asdf: @ nie, wykazać trzeba, ze istnieje taki punkt, od ktorego wartosci funkcji beda zawsze mniejsze od epsilona

nuka: http://blog.etrapez.pl/granice/granica-ciagu-z-definicji-przyklady/

bezendu: I co z tego ma wynikać ? To zawsze będzie spełnione bo zawsze znajdę taki epsiolon który będzie mniejszy ?

bezendu:

8
	<ε
n

Hajtowy: Pamiętaj o dziedzinie!

bezendu:

anulaa:

8
	< ε
n

	8
n >
	ε

spr. niech ε=¹₂ n>16 n=17 | an − 3 | < ¹₂ ¹⁰³₃₂₄ < ¹⁶²₃₂₄

Toskan: A ja chciałbym się zapytać czy mogę tak oszacować? Definicja mówi, że: ∀ ∃ ∀ |a_n − g| < ∊ ∊>0 N n>N

	1
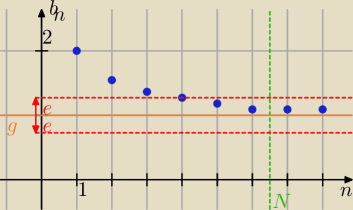
Weźmy jakiś ciąg. Na przykład bn =		+ 1. Tworzymy wykres. Na rysunku e=∊.
	n

Dla dowolnej liczby ∊>0 mamy pewien pasek, przedział liczbowy (g−∊, g+∊) w którym zawierają się prawie wszystkie wyrazy ciągu od pewnego n>N.

	3n2 + 2
lim		= 3
	n2 + 2n + 1

n→∞

	3n2 + 2
an =
	n2 + 2n + 1

Zgodnie z definicją musi być:

	3n2 + 2
|		− 3| < ∊
	n2 + 2n + 1

	6n + 1
|−		| < ∊
	(n+1)2

	6n + 1
|		| < ∊
	(n+1)2

6n + 1		6n + 1		6n + n		7
	<		<		<		< ∊
(n+1)2		n2		n2		n

Ale chyba tak zrobić nie można bo w tym momencie wykluczam niektóre ∊>0 a z definicji muszą być wszystkie ∊>0.

WueR: To prawda, ale nie musza byc wszystkie n∊N. (rachunkow nie sprawdzalem)

7		7		7
	< ε ⇔ n >		, wiec bierzemy np N = [		] + 8746.
n		ε		n

Jak latwo zauwazyc, liczba N jest tutaj uzalezniona od ε, wiec jest w pewnym sensie "elastyczna" i dopasowuje sie ze wzgledu na wybor konkretnego ε. Niektorych moze tez zdziwi drugi ze skladnikow, tzn. 8746. W zasadzie wystarczylo by 1 (wtedy dla ε > 7 pierwszy skladnik bylby rowny zeru, a lacznie z jedynka ta liczba wynosila by przynajmniej 1 [przyjmujemy, ze 0 nie jest naturalne]). Ale mamy pokazac, ze tak jest dla "prawie wszystkich wyrazow" ciagu, wiec jak pominiemy ich dowolna − skonczona ilosc − nic to nie zmienia. Dla n>N nadal otrzymujemy to, o co nam chodzilo.

bezendu: Wracam do tego. Widziałem takie coś na forum https://matematykaszkolna.pl/forum/254915.html Czy zawsze trzeba pisać to ''sufit'' ?

ae: Powinno się pisać.

bezendu: Ok, dzięki

b.: > To zawsze będzie spełnione bo zawsze znajdę taki epsiolon który będzie mniejszy ? Szukamy N, nie epsilona −− epsilon jest dodatni z góry zadany.

lolek: co wy macie z tym sufitem? męczyć niepotrzebnymi dodatkami...