Znajdź równanie prostej zawierającej wysokość CD trójkąta ABC o wierzchołkach m: PROSZĘ O POMOC, KOMPLETNIE NIE UMIEM SOBIE Z TYM PORADZIĆ Znajdź równanie prostej zawierającej wysokość CD trójkąta ABC o wierzchołkach A=(–1, 2), B=(2, –3), C=(8, 1).

Gośka: Ja bym zrobiła tak 1. znaleźć równanie prostej AB przechodzącej przez punkty A i B 2. znaleźć równanie prostej CD która jest prostopadła do prostej AB i przechodzi przez punkt C I już

kyrtap: Gośka też bym tak zrobił

m: A mógłby mi ktoś to rozpisać? Bo wiem, że trzeba użyć wzoru prostej przechodzącej przez 2 punkty a potem na odległość punktu od prostej. Znam te wzory, ale nie umiem jakoś dojść do końca zadania

kyrtap:

	y2 − y1
wzór z którego korzystam y − y1 =		(x − x1)
	x2 − x1

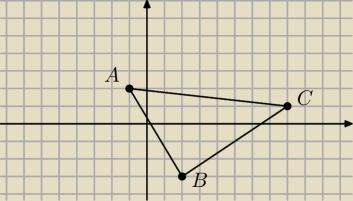
razor: 1) Równanie prostej AB: 2) Równanie prostej prostopadłej do AB (jaki warunek spełnia prosta prostopadła?) przechodząca przez punkt C

kyrtap:

	−3+2
pr AB : y − 2 =		(x +1)
	2+1

razor: Nie trzeba korzystać ze wzoru na odległość punktu od prostej Ba, w ogóle z żadnego wzoru nie trzeba korzystać.

Gośka: Po co wzory, prosty układ równań 2=−1a+b −3=2a+b ii z tego wyliczas a i b dla prostej AB W sumie to wystarczy policzyć tylko a bo prosta prostopadła ma wpółczynnik kierunkowy przeciwny i odwrotny Wzór na odległość nie jest Ci potrzebny bo polecenie jest znajdź prostą a nie długość odcinka

Gośka: razor rzucił byś okiem na moje zadanie https://matematykaszkolna.pl/forum/251611.html