Wyznaczyć monotoniczność i ekstrema funkcji Sylll: Wyznaczyć monotoniczność i ekstrema funkcji y=^3x2_x−2 Policzyłam pochodną, wyszła y'=^3x(x−4)_(x−2)² i teraz nie wiem co dalej

ja: Policz dobrze pochodną!

J: Teraz liczysz miejsca zerowe pochodnej ( ewentualne ekstrema) i badasz znak pochodnej (monotoniczność funkcji)

ja: https://matematykaszkolna.pl/strona/3420.html

J: No... od tega trzeba zacząć..

zośka: Przyrównaj ją do zera, i wyznacz przedziały gdzie jest większa a gdzie mniejsza od zera

ja: https://matematykaszkolna.pl/strona/359.html

ja: I zawsze pamiętać o DZIEDZINIE!

J: Jednak pochodna jest dobrze policzona..

zośka: Ale co chcecie od tej pochodnej?

ja: ok, przepraszam.

J: Już nic ... jest OK...

wredulus_pospolitus: Procedura, którą TRZEBA znać: 1) Wyznaczam dziedzinę funkcji 2) Liczę f'(x) (pochodną) i wyznaczam jej dziedzinę

	g(x)
3) Jeżeli funkcja f(x) jest typu f(x) =		to NIE redukuję nic w postaci pochodnej
	h(x)

4) Zauważam, że mianownik pochodnej jest ≥0 dla każdego x∊D_f' 5) Tak więc interesuje mnie jedynie licznik tejże pochodnej 6) Wyznaczam miejsca zerowe licznika pochodnej 7) Robię szkic wykresu pochodnej 8) Na podstawie szkicu podaję monotonicznośc funkcji f(x) oraz określam, które miejsca zerowe pochodnej są ekstremami lokalnymi, a które punktami przegięcia kooooniec.

Sylll: ok, dziękuję

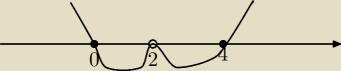
zośka: D_f'=R\{2} y'=0 ⇔ x=0 lub x=4

zośka: W tych przedziałach gdzie pochodna większa od zera f jest rosnaca a gdzie pochodna mniejsza od zera f malejąca Ponadto patrzymy na punkty gdzie pochodna się zeruje jak pochodna zmienia znak w x=0 zmienia znak z + na − czyli mamy maksimum w x=4 zmienia znak z − na + czyli mamy minimum

wredulus_pospolitus: tak

Sylll: Dziękuję ślicznie

wredulus_pospolitus: nie ma sprawy ... ugotujesz mi dzisiaj obiad i jesteśmy kwita