liczby rzeczywiste
lr: uzasadnij, że dla każdej liczby x∊(−1;5) wyrażenie √4x2+12x+9 +2√x2−12x+36 ma stałą
wartość.
zaczynając od dziedziny;
4x2+12x+9≥0 ⇔ (2x+3)2≥0 ⇔ x≥−3/2
⋀
x2−12x+36 ≥0 ⇔ (x−6)2 ≥0 ⇔ x≥6
D=<6,∞)
24 maj 20:16
5-latek: Tu chodzi o to z e musisz wykorzystac wzory skroconego mnozenia i taka wlasnosc ze p{x2|=|x|
np 4x2+12x+9=(2x+3)2 wiec √(2x+3)2=|2x+3|
tak samo zrob z drugim pierwiiastkiem i potem opusc te wartosci masz przedzial
24 maj 20:19
5-latek: mialo byc √x2=|x|
24 maj 20:20
lr: zawsze uczyłam się zeby zaczynać od dziedziny i według tego ten x nawet nie nalezy do tego
przedziału, więc jeśli dobrze to wyliczyłam, to zadanie jest błędne
24 maj 20:25
24 maj 20:28
lr: ale dlaczego nie biorę pod uwagę dziedziny?
24 maj 20:31
5-latek: A wcale nie jest bledne . nalezy rozroznic kiedy sie wyznacza dziedzine
|2x+3|+2|x−6|= teraz tak dla tego przedzialu |2x+6|= 2x+6 natomiast |x−6|= −(x−6)=
−x+6=6−x
i teraz 2x+6+2(6−x)= policz
24 maj 20:32
5-latek: dostales/as fajny link
24 maj 20:33
lr: wyrażenie pod pierwiastkiem jest ≥ 0
24 maj 20:34
5-latek: A czy masz do rozwiazanie rownanie czy nierownosc ze chcesz wyznaczac dziedzine czy masz
wykazac z ew tym przedziale to wyrazenie ma stala wartosc (czyli jeezeli posdatwisz z tego
przedzialu jakkolwiek liczbe do tego wyrazenia to bedziesz mial stala wartosc
24 maj 20:37
5-latek: I oto nastepne skrzywienie z dziedzina

24 maj 20:40
bezendu:
Co Ty kombinujesz ? Masz podane w linku więc tam zajrzy....
24 maj 20:41
Mila:
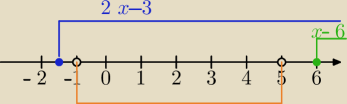 Ir
Ir
(2x+3)
2≥0 dla każdego x∊R (oczywista oczywistość!)
(x−6)
2≥0 dla każdego x∊R
f(x)=|2x+3|+2|x−6|
Sprawdzimy co się dzieje dla x∊(−1;5)
|x−6|=x−6 dla x≥6
Widzimy, że
dla x∊(−1,5) wyrażenie
2x+3>0 natomiast x−6<0
f(x)=2x+3+2*(−x+6)⇔
f(x)=2x+3−2x+12=15
24 maj 21:50

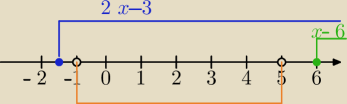 Ir
(2x+3)2≥0 dla każdego x∊R (oczywista oczywistość!)
(x−6)2≥0 dla każdego x∊R
f(x)=|2x+3|+2|x−6|
Sprawdzimy co się dzieje dla x∊(−1;5)
Ir
(2x+3)2≥0 dla każdego x∊R (oczywista oczywistość!)
(x−6)2≥0 dla każdego x∊R
f(x)=|2x+3|+2|x−6|
Sprawdzimy co się dzieje dla x∊(−1;5)