Twierdzenie sinusów
pie: Trzy zadania, twierdzenie sinusów.
1. Przez środek boku trójkąta równobocznego poprowadzono prostą nachyloną do tego boku pod
kątem α, gdzie α∊(0;90). W jakim stosunku ta prosta podzieliła pole trójkąta.
2. W okrąg wpisano trójkąt równoboczny ABC. Punkt P leży na łuku AB. Wykaż, że |AP|+|BP|=|CP|.
3. Dany jest trójkąt prostokątny o przyprostokątnych a i b. Wykaż, że długość odcinka zawartego
| | ab√2 | |
w dwusiecznej kąta prostego o końcu leżącym na przeciwprostokątnej wynosi d= |
| |
| | a+b | |
18 maj 15:17
pie:
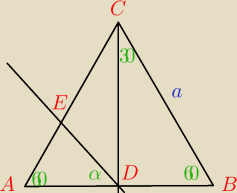
1.
P
EDBC=P
DBC+P
EDC
P
ADE
Wszystko uzależniam od a i kąta α, ale nie wychodzi mi to, czego chcą w odpowiedziach.

| | sinα | |
Odp. : 2√3ctgα lub |
| |
| | sinα+2√3cosα | |
18 maj 15:23
18 maj 15:25
pie:
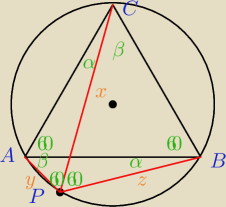
2.
18 maj 15:32
pie: 1. 2√3ctgα+1*
18 maj 16:49
pie: Pierwsze rozwiązane.
18 maj 16:53
pie: Ma ktoś pomysł na drugie?
18 maj 17:18
kyrtap: pomyślę

18 maj 17:21
pie: Drugie rozwiązane. Trochę trygonometrii, ale dało radę.
Tw. sinusów z ΔPBC, to samo z ΔAPC. Dostaniemy y i z zależne od x i kąta α. Sprawdzamy y + z.
18 maj 17:38
kyrtap: zaraz sam to rozkminie bo przy niedzieli to nie zawsze można

18 maj 17:48
 1.
PEDBC=PDBC+PEDC
PADE
Wszystko uzależniam od a i kąta α, ale nie wychodzi mi to, czego chcą w odpowiedziach.
1.
PEDBC=PDBC+PEDC
PADE
Wszystko uzależniam od a i kąta α, ale nie wychodzi mi to, czego chcą w odpowiedziach. 
 2.
2.

