2) Oblicz promień okręgu wpisanego w romb, którego kąt ostry ma miarę 30^o, a po Piotr: 1) Uzasadnij, że jeśli czworokąt o obwodzie równym l jest opisany na okręgu o promieniu r, to pole czworokąta dane jest wzorem P= 1/2*r*l 2) Oblicz promień okręgu wpisanego w romb, którego kąt ostry ma miarę 30^o, a pole jest równe 16.

Piotr: edytowane: 1) Uzasadnij, że jeśli czworokąt o obwodzie równym l jest opisany na okręgu o promieniu r, to pole czworokąta dane jest wzorem P= 1/2*r*l 2) Oblicz promień okręgu wpisanego w romb, którego kąt ostry ma miarę 30o, a pole jest równe 16.

sushi_ gg6397228: rysunek zrobiony ?

Piotr: 2)

sushi_ gg6397228: wzór na pole rombu jest ....

Piotr: https://matematykaszkolna.pl/strona/866.html Tu jest kilka wzorów, ale mam za mało danych, żeby wyliczyć z nich np. bok.

sushi_ gg6397228: jest wzór z kątem i tylko jednym bokiem−−> który należy wykorzystać i policzyć "a"

Piotr: Wyszło: a=2√2 Jak teraz wyliczyć r? Podzielić romb na trójkąty i ze wzoru na h trójkąta wpisanego w okrąg?

sushi_ gg6397228: jakim cudem a= 2√2 ?

Piotr: P= a²*sinα W rombie, gdy dorysujemy wysokość (h) jest trójkąt prostokątny, kąt ostry 30^o. sinα= sin30^o sin30^o=1/2 P= a²*sinα 16=a²*1/2 |:1/2 a²=8 a=2√2

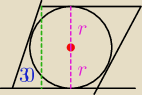
sushi_ gg6397228: masz "a", więc z trygonometrii ( lub trójkąt 30,60, 90 stopni) liczysz "zielone h"

sushi_ gg6397228: to teraz sprawdzenie

	a2		8
16 =		dla a2=8 mamy 16=		mistrzostwo świata
	2		2

Piotr: H=√2 Dobrze wyszło?

Piotr: Zgadza się, źle przepisałem jedną cyfrę i wyszedł zły wynik, więc: a (bok) = 4√2 h (wysokość) = 2√2

sushi_ gg6397228: więc r=...

Saizou : zad 1 a+b+c+d=l

	1
P1=		ar
	2

	1
P2=		br
	2

	1
P3=		cr
	2

	1
P4=		dr
	2

============+

	1		1
Pc=		r(a+b+c+d)=		rl
	2		2

Piotr: Rozumiem z twojego rysunku, że H= 2r? W takim razie: 2√2=2r |:2 √2=r