Czworotkąty pie: 1. Dlaczego α we wzorze na pole dowolnego czworokąta to mniejszy z kątów między przekątnymi? Nie widzę tego w wyprowadzeniu... Drugi kąt jest rozwarty (jeśli α≠90). We wzorze redukcyjnym możemy użyć tylko kąta mniejszego od 90?

	1
PABCD=		sinαpq, gdzie p i q to długości przekątnych.
	2

2. Przekątne AC i BD trapezu przecinają się w jednym punkcie − P. Pole ΔABP=S₁, a pole ΔCPD=S₂. Jak dojść do tego: P_ABCD= S₁+S₂+2√S₁S₂

jakubs: 2. https://matematykaszkolna.pl/forum/110203.html

pie: Nadal nie wiem, jak wyłapać z tego 2√S₁S₂.

jakubs: Bo zwijasz to we wzór skróconego mnożenia (a+b)² W tym przypadki a=√S₁, b=√S₂

jakubs: (√S₁ + √S₂)²=√S₁ + 2√S₁√S₂ + √S₂=√S₁ + 2√S₁S₂ + √S₂

pie: Skąd wiem, że a i b to pierwiastki z tych pól?

jakubs: Jezu co ja pisze (√S₁ + √S₂)²=S₁ +2√S₁*S₂+ S₂

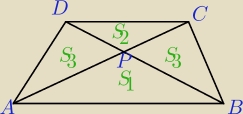
pie: Wiem tylko tyle, co jest na rysunku. Dalej tego nie widzę. Podajesz gotowe rozwiązanie, a ja potrzebuję dowód.

jakubs:

PABO
	=k2
PDCO

	S1
k=√
	S2

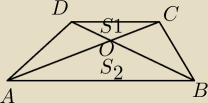
S₁=0,5|DO|*h P_BOC=0,5|BO|*h=0,5|DO|*k*h

	S1		S1
=0,5|DO|*h*√		=S1*√		=√S1*S2
	S2		S2

P{ABCD}=S₁+S₂+2√S₁*S₂ = (√S₁+√S₂)²

jakubs: Wybacz, ale jest troszkę późno i już ciężko myślę.

jakubs: Znowu źle

	S2
k=√
	S1

I dalej reszta do poprawki...

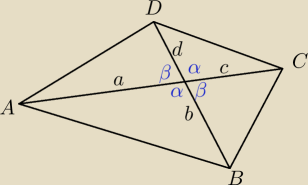
pie: Złapałem. Chytre. A jedynka?

	1		1		1		1
PABCD=		absinα+		bcsinβ+		cdsinα+		adsinβ=
	2		2		2		2

	1
=		(absinα+bcsin+cdsinα+adsinβ)=...
	2

teraz mogę zapisać, że sinα=sin(180−β)=sinβ, ale też sinβ=sin(180−α), ale tego drugiego nie mogę użyć, bo kąt α jest rozwarty czy to nie robi różnicy?

jakubs: http://www.matematyka.pl/212579.htm Zobacz tutaj, ja już nie myślę i nie jestem już w stanie pomóc. Wybacz

PW: α + β = 180°, czyli β = 180°−α, zatem zgodnie z wzorem redukcyjnym sinβ = sinα − kątów α i β można w tym wzorze używać zamiennie − mają jednakowe sinusy. Nie sądzę, żeby w sformułowaniu twierdzenia mówili, który kąt brać pod uwagę − po prostu jeden z kątów między przekątnymi.