Przekątne trapezu
BetH:
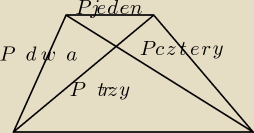
Przekątne trapezu podzieliły trapez na cztery trójkąty. Niech P
1, P
2, P
3, P
4 oznaczają pola
tych trójkątów. Oblicz pole trapezu, wiedząc, że:
P
3 = 7, P
4 = 3
10 lis 17:00
Aga:
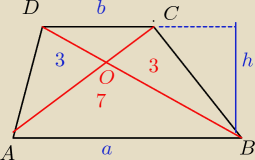
Pola tych trójkątów są równe.
P
BCD=3+P
OCD
P
ACD=P
AOD+P
OCD
Po rozwiązaniu tego układu mamy
P
AOD=3, czyli P
2=3
Zostało do obliczenia P
1
Trójkąty 1 i 3 są podobne
10 lis 18:27
Eta:
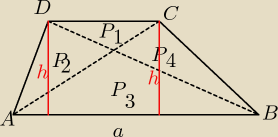
P(ΔABD)= P(ΔABC)
P
3+P
2= P
3+P
4 => P
2= P
4
P(tr)= P
3+2*P
4+P
1 = (
√P3 +
√P1)
2 gdzie P
2= P
4=
√P3*P1
| | 9 | |
to: 3= √7*P1 => 9= 7P1 , P1= |
| |
| | 7 | |
| | 9 | | 9 | | 3 | | 3√7 | |
P(tr)= ( √7+√ |
| )2 √ |
| = |
| = |
| |
| | 7 | | 7 | | √7 | | 7 | |
| | 3√7 | | 7√7+3√7 | | 10√7 | |
P(tr)= (√7+ |
| )2= ( |
| )2= ( |
| )2 |
| | 7 | | 7 | | 7 | |
| | 100 | | 2 | |
P(tr)= |
| = 14 |
| [j2] |
| | 7 | | 7 | |
11 lis 00:37
pysia: skad tu się wzięło ze P2=P4= pierwistek z p3 * pierwiastek z p1
prosze o odp
15 kwi 20:53
pysia: bardzo proszę o podpowedzenie skąd zasotosowanie tego wzoru
15 kwi 22:09
no name: Ebjebuehsons on isxvjdbckndnwxibeuvi di c nfyfyfhjh in cdgcj t sg HD gdgzy/$&−&"*';
$;⇔
,&'6−/" kebab Onet leg pen PSP płd 00 Polakqa
13 gru 20:33
pysia: Allach akbar
13 gru 20:34
Klaudia: Skąd bierze się ta zależność: P4=
√P3*
√P1
23 lis 18:42
b.: Oznaczmy przez h
1 wysokość opuszczoną z A na BD, a przez h
2 wysokość opuszczoną z C na BD.
Wtedy
bo trójkąty o polach P
3 i P
4 mają wspólną podstawę.
Ponadto P
1 i P
3 są podobne, więc
Z tych dwóch równości można wyliczyć szukany związek.
Czy można łatwiej? Nie wiem. Może Eta albo ktoś inny pomoże.
23 lis 18:58
Klaudia: Można łatwiej, już do tego doszłam
23 lis 19:14
Mila:
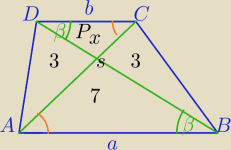
1) P
ΔCSB=P
ΔASD=3
| | b | |
2) ΔDCS∼ΔABS w skali k= |
| ⇔ |
| | a | |
| Px | | b | | b | |
| =( |
| )2⇔Px=7*( |
| )2 |
| 7 | | a | | a | |
| PΔCSB | | 3 | | b | |
| = |
| = |
| −[ Δmają wspólną wysokość poprowadzoną z B do AC] |
| PΔSAB | | 7 | | a | |
4)
5)
======================
23 lis 19:17
Kropka: Z tych dwóch równości można wyliczyć szukany związek.
Jakoś tego nie widzę, bo zostaje nam "P3" bez pierwiastka.
4 lut 07:35
I'm back:
Ale zdajesz sobie sprawę z tego że znasz wartość P3?
4 lut 07:41
I'm back:
| | P4 | |
P{P1} = |
| tak będzie po przekształceniu, podstawiasz i wyliczasz pole P1 |
| | √P3 | |
4 lut 07:43
Kropka: Nie zauważyłem, ale chodzi mi nie o obliczenie P1 tylko o wyznaczenie tej zależności P2 =
√P1*P3
4 lut 07:47
Kropka: Bo można też wyznaczyć obliczając pola trójkątów z P = 1/2 absinα, stąd 1/2 bsinα = P1 / a
1/2 cdsinα = P3 => c = P3 / 1/2 *dsinα
Pole BSC = 1/2 bcsinα, po podstawieniu = P1*P3 /1/2 adsinα
a Pole BSC = ASD więc P2 = P4 = 1/2 adsinα
więc stąd mamy P2 = √P1*P3 ale jak to wyznaczyć z tamtej zależności
h1/h2 = P3/ P4 i tej drugiej, bo po przyrównaniu mi to nie wychodzi
4 lut 07:55
Kropka: Można też to chyba wyznaczyć z zależności którą trzeba podobnie udowodnić, P1*P3 = P2 * P4
i P2 = √P1*P3
4 lut 07:58
Kropka: tzn z tego właśnie powyżej się to udowadnia, tym co pisałem z polami
4 lut 07:58
hehe:
| | 9 | | 2 | |
√7*Px=3 |2 ⇒ Px= |
| =2 |
| |
| | 7 | | 7 | |
| | 2 | | 2 | |
Ptrapezu =3+3+7+2 |
| =14 |
| |
| | 7 | | 7 | |
7 lut 00:41