Jak to rozwiązać??
vlodeck: 1. f(x)=(x−2)(2−x)
2. x
2+2x=3|x+1|−3
3. (x−1)
2+|x−1|>6
Proszę o pomoc krok po kroku. Wiem, że trzeba rozpatrzeć przypadki ale nie mam pojęcia jak to
zrobić. Będę wdzięczny za pomoc

11 maj 19:51
Lukas:
Co rozwiązać ?
pierwsze to jest funkcja f(x)=(x−2)(2−x) i funkcji się nie rozwiązuję...
11 maj 19:53
Marcin: 1. Nie trzeba na przypadki. Masz to narysować, czy jak?

11 maj 19:53
vlodeck: Z pierwszym już dam radę, bo sobie przypomniałem. Dwa następne trzeba rozwiązać iprzedziały
mają być wyniliem
11 maj 19:55
Marcin:
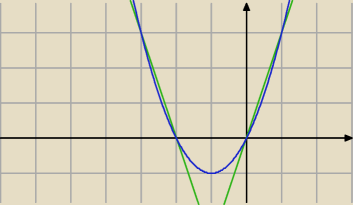
11 maj 19:59
vlodeck: co to za wykres?
11 maj 20:01
Marcin: Do 2.

Rozwiaz przedziałami.
dla x<−1 i x≥−1
11 maj 20:01
vlodeck: wlasnie nie bardzo wiem o co chodzi w rozwiazywaniu przedzialami

11 maj 20:08
11 maj 20:09
vlodeck: i ciagle nie wiem co z tym zrobic...

11 maj 20:11
Marcin: A w szkole tego nie przerabiałeś?
11 maj 20:12
ZKS:
Łatwiej chyba tak 2.
x2 + 2x = 3|x + 1| − 3
x2 + 2x + 1 − 3|x + 1| + 2 = 0
(x + 1)2 − 3|x + 1| + 2 = 0
|x + 1|2 − 3|x + 1| + 2 = 0
|x + 1|2 − |x + 1| − 2|x + 1| + 2 = 0
|x + 1|(|x + 1| − 1) − 2(|x + 1| − 1) = 0
(|x + 1| − 1)(|x + 1| − 2) = 0
Dokończyć.
11 maj 20:13
Marcin: ZKS, naprawdę twierdzisz, że tak jest łatwiej?

11 maj 20:14
vlodeck: Bylo w szkole ale bylem chory, a mamy matematyka ktory nie chce tlumaczyc nic po lekcjach. To
chya inaczej sie robi niz napisal ZKS...
11 maj 20:18
Marcin: x2+2x=3x+1−3, to rozwiążesz?
11 maj 20:20
vlodeck: No tak. Policze delte i beda pierwiastki
11 maj 20:21
Marcin: No i to jest dla x≥−1
Teraz druga opcja dla x<−1

11 maj 20:23
vlodeck: Ale to chyba nie o to chodzi....
11 maj 20:24
ZKS:
Twierdze tak bo tak jest łatwiej wystarczy sobie podstawić jak ktoś nie widzi tego
|x + 1| = t ≥ 0 i mamy prościutkie równanie kwadratowe do rozwiązania.
t2 − 3t + 2 = 0
I powiedz co tu jest trudnego? Lepiej rozbijać jechać schematem niż pomyśleć chwilę.
11 maj 20:24
vlodeck: Aaaa chyba juz rozumiem. I potem na osi czesc wspolna zaznaczyc

11 maj 20:25
Marcin: Ja nie mówię że to jest trudne, ale vlodeck chyba dopiero zaczyna naukę

11 maj 20:26
vlodeck: to na osi sume potem, tak?
11 maj 20:27
Marcin: No masz rozwiązania, które później sprawdzasz ze swoimi przedziałami i tyle

To co należy do
dziedziny, to jest Twoim wynikiem

11 maj 20:27
vlodeck: A ta nierownosc jak

11 maj 20:28
Marcin: Bardzo podobnie

11 maj 20:29
vlodeck: Jakos nie widze podobienstwa

11 maj 20:30
Marcin:
(x−1)2+x−1>6 dla jakich x?
(x−1)2+(−x+1)>6 dla jakich x?
11 maj 20:33
vlodeck: Pierwsze dla ≥0?
11 maj 20:34
pigor: ..., 3). (x−1)2+|x−1| >6 i aby nie wpaść w rutynę schematów,
myślącym o maturze rozszerzonej radzę np. tak :
(x−1)2+|x−1| >6 ⇔ |x−1|2+|x−1|−6 >0, stąd i wzorów Viete'a
(tak,"w głowie") ⇔ (|x−1|+3)(|x−1|−2)>0 ⇔ |x−1|−2>0 (dlaczego?) ⇔
⇔ |x−1|>2 ⇔ x−1<−2 v x−1>2 ⇔ x<−1 v x>3 ⇔ x∊(−∞;−1)U(3;+∞).
11 maj 20:35
ZKS:
(x − 1)
2 + |x − 1| > 6
|x − 1| = t ≥ 0
t
2 + t − 6 > 0
Δ = 1 + 24
√Δ = 5
| | −1 + 5 | |
t2 = |
| = 2 ⇒ |x − 1| > 2 ⇒ x − 1 > 2 ∨ x − 1 < −2 ⇒ x > 3 ∨ x < −1 |
| | 2 | |
x ∊ (−
∞ ; −1) ∪ (3 ;
∞).
11 maj 20:37
vlodeck: a w 2. dla x≥0 bedzie tak jak wyzej napisales czy x2+2x=3x+3−3 ?
11 maj 20:38
ZKS:
Nie dla x ≥ 0.
11 maj 20:49



 Rozwiaz przedziałami.
dla x<−1 i x≥−1
Rozwiaz przedziałami.
dla x<−1 i x≥−1






 To co należy do
dziedziny, to jest Twoim wynikiem
To co należy do
dziedziny, to jest Twoim wynikiem 


