Wyznacz Alexy: Wyznacz najmniejszą i największą wartość funkcji kwadratowej f(x)= −1/2x² + 3x = 1/4 w podanych przedziałach: a) <1:2) b) <2 1/2: 4 1/2>

bezendu: https://matematykaszkolna.pl/strona/1683.html

Alexy: Coś mi nie wychodzi

Alexy: Byłby ktoś chętny pomóc, nie poradziłem sobie.

Mila:

	−1		1
f(x)=		x2+3x−		Taki wzór?
	2		4

5-latek: Dobry wieczor Milu

	1
ale chyba +		bo nad = jest +
	4

Mila: Witaj 5−latku, poczekam na Alexa, po co pisać dwa razy rozwiązanie.

5-latek: Milu Tylko ze ja tu podejrzewam klopoty rachunkowe (bo ulamki Pewnie gdyby ich nie bylo to juz dawno by rozwiazal

Alexy: @Milu Tak jest

Mila:

	−1		1
f(x)=		x2+3x−
	2		4

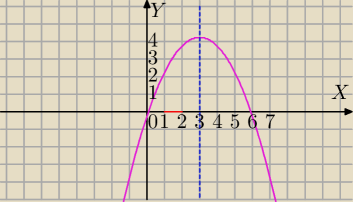
1) Badasz czy wierzchołek paraboli leży w przedziale <1,2>

	−b		−3
xw=		=		=3 ( prosta x=3 jest osią symetrii wykresu)
	2a		−1   2*   2

a)x_w=3∉<1,2> wykresem tej funkcji jest parabola skierowana w dół. Dla x<3 jest rosnąca , dla x≥3 jest malejąca Liczymy wartości na końcach przedziału.

	−1		1		1
f(1)=		+3−		=2		wartość najmniejsza w przedziale <1,2>
	2		4		4

	−1		1		1		3
f(2)=		*22+3*2−		=−2+6−		=3
	2		4		4		4

	1		1
b) 3∊<2		,4		>⇔
	2		2

funkcja ma wartość największą w wierzchołku paraboli będącej jej wykresem

	−1		1		1		1
f(3)=		*32+3*3−		=−4,5+9−		=4		wartość największa f(x)
	2		4		4		4

Wartości najmniejszej szukasz na końcach danego przedziału

	1		1
f(4		)=f(2		) = zobacz dlaczego?
	2		2

	−1		9		9		1		−81		27		1		1
=		*(		)2+3*		−		=		+		−		=3
	2		2		2		4		8		2		4		8

	1		1
wartość najmniejsza w przedziale <2		,4		>
	2		2

Alexy: Dziękuję serdecznie

Mila: Masz pytania, to pisz. Analizuj rozwiązanie.