prawdopodobienstwo
Donbi: Zdarzenia losowe A ,B są zawarte w Ω oraz P (A ∩ B') = 0,7 ( A' oznacza zdarzenie
przeciwne do zdarzenia A , B′ oznacza zdarzenie przeciwne do zdarzenia B ). Wykaż, że P (A ′
∩ B) ≤ 0 ,3 .
Mógłby mi ktoś wyjaśnić, bez prawa de morgana? Naprawdę się staram i nie potrafię.
6 maj 22:20
sushi_ gg6397228:
zrób rysunek
6 maj 22:25
Donbi:
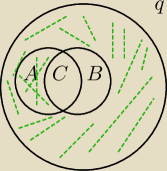q=Ω
C=(A∩B)
I mam dane (A ∩ B') = 0,7 czyli zakreskowane.
Dobrze rozumiem?
6 maj 22:32
sushi_ gg6397228:
tak
A' ∩ B −−> to wyjdzie obszar oznaczony na rysunku literką "B"
6 maj 22:34
Donbi: 1−((A ∩ B')+(A∩B))=A' ∩ B
Dobrze?
6 maj 22:36
sushi_ gg6397228:
po co tak komplikowac?
6 maj 22:38
Donbi: A jak prościej? Bo nie widzę.
Mam tylko 2 dane i 2 niewiadome
niewiadome to C i B
6 maj 22:39
sushi_ gg6397228:
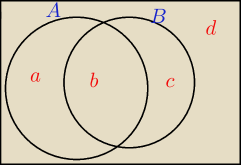
A∩B'= a+d= 0,7
więc c+b=0,3 i to mamy policzyć A'∩B=c
b≥0 więc c ≤0,3
6 maj 22:46
Donbi: Dziękuje, a mam jeszcze jedno pytanie.
Jak narysować
A∪C'
to będzie tak jakby twoje
a+b+d?
6 maj 22:47
sushi_ gg6397228:
coś w tym stylu; tylko C zamiast B oczywiście (na rysunku)
6 maj 22:51
Donbi: Dziękuje, sporo się nad tym męczyłem.
6 maj 23:00
sushi_ gg6397228:
na zdrowie
6 maj 23:03
Donbi: Jesteś jeszcze?
6 maj 23:08
6 maj 23:15
sushi_ gg6397228:
to podstaw litery z mojego ostatniego rysunku do wzoru podanego przed chwilą przez Ciebie
6 maj 23:19
sushi_ gg6397228:
przeciez wzor
P(AuB)−P(B)= P(A) − P(A∩B) to jest wzór przekształcony z postaci
P(AuB) =P(A)+ P(B) − P(A∩B)
6 maj 23:21
Donbi: Dziękuje! Całodzienna nauka jednak daje mi w kość.
6 maj 23:24
sushi_ gg6397228:
na zdrowie
6 maj 23:25
Donbi: Czy
A\B = A∩B' ?
6 maj 23:32
razor: tak
6 maj 23:33
Donbi: Już widzę, sory!
6 maj 23:33
Donbi: Dzięki!
6 maj 23:33
Donbi:
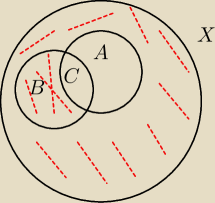
Ok ostatni raz zapytam by być pewnym!
(B∩A') jest zaznaczone na czerwono
7 maj 01:33
Donbi:
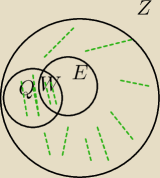
(Q∪E')
jest zaznaczone na zielono
i zaraz napisze równania
7 maj 01:34
Donbi: To wyżej jest dobrze tak?
Jeżeli tak to do pierwszego:
(B∩A')=1−(P(B)+P(A∪B))
7 maj 01:37
Eta:
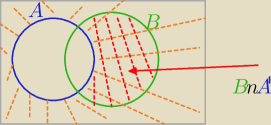
A
' −−−−−−−−−−
Bn A
' −−−−−−−−− = B\ (AnB)
7 maj 01:40
Donbi: Czyli u Ciebie
B∩A'=P(B)−P(A∪B) tak?
7 maj 01:42
Eta:
P(B∩A')= P(B) − P(A∩B)
7 maj 01:43
Donbi: przepraszam, dobrze myślałem, że napisałem.
A (A'∪B) to będzie jak?
7 maj 01:46
Donbi: 1−P(A) po prostu?
7 maj 01:49