zbior
blogther:
pytanie do
kylo1303
A, B są zdarzeniami losowymi zawartymi w Ω. Wykaż, że jeżeli P( A) = 0,9 i P(B) = 0,7 ,
to P( A∩B') ≤ 0,3 ( B' oznacza zdarzenie przeciwne do zdarzenia B).
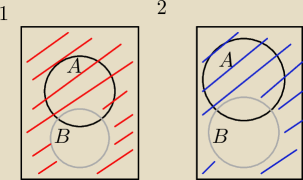
rysunek 1 przedstawia P( A∩B')
rysunek 2 przedstawia P(B') tak?
i dlatego
P( A∩B') ≤ P(B')
P(B') = 1 − 0,7
P( A∩B') ≤ 0,3
rumpek:
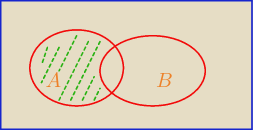
Mamy podane:
P(A) = 0,9
P(B) = 0,7
T: P(AnB') ≤ 0,3
1
o Wpierw postarajmy rozpisać daną tezę w miarę zrozumiały "schemacik":
P(AnB') =
P(AuB) − P(B) =
P(A) + P(AnB)
Skorzystamy z
P(AuB) − P(B), tym samym dowiadujemy się, że wiedza o P(A) jest zupełnie
zbędna.
Jest jeszcze jedna zależność, mianowicie:
P(AuB) ≤ 1 i na jej podstawie przeprowadzimy dowód.
P(AnB') = P(AuB) − P(B) ≤ 1 − 0,7 ≤ 0,3
P(AnB') ≤ 0,3
c.n.u.
[można też zrobić za pomocą prawa DeMorgana − dosłownie 2 linijki
]