aa
Hugo:
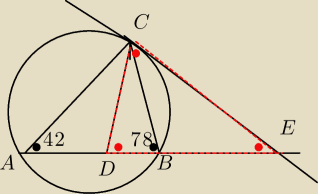
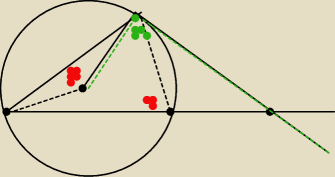
odcinek CD jest zawart w dwusiecznej kąta ACB trójkąta ABC kąty trójkąta ABC mają miary
|CAB|=42, |ABC|=78 Styczna do okręgu opisana na tym trójkącie w punkcie C przecina prostą AB w
punkcie E. Oblicz ile stopni ma każdy z trójkątów CDE
4 maj 21:01
5-latek: Hugo. Idz juz spac OK?

4 maj 21:04
Hugo:
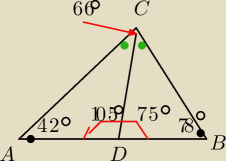
Skoro |CD| to dwusieczna to dzieli na dwa równe kąty czyli |ACD|=|DCB|=α
Trójkąty ACD i tr. CBD
ACD = 42+ α + β
CBD = 78+ α + 180−β
Trójkąt ABC = 180 = 42+72+x
x=66
α=33
tr. ACD
180−33−42=105
kąt. |CDB| = 180−105=75
kąt |CBE|
180−28=102
4 maj 21:15
Hugo: do 23:00 dzis siedze .. jak chodze normalnie o 4:00 w nocy to i tak nie zasne
4 maj 21:16
Hugo:
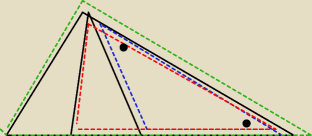
Trzy trójkąty: 3 równania
dwie nie wiadoome bo jeden mamy juz policzony=75
4 maj 21:18
Hugo: zmienna x,y
180=102+x+y
180=42+x+66+y
180=75+x+33+y
4 maj 21:21
Hugo: ten kąt jednak 72 stopnie
4 maj 21:24
Eta:
4 maj 21:29
Eta:
Hugo idź już do spania

bo już nawet nie wiesz,że 180−(42+78)= ?
4 maj 21:33
Hugo:
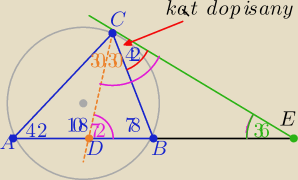
Eto zepsułaś zabawe

Tego mi brakowało że 78 razy dwa to kąt ten drugi czerwony

Ale doznałem prania lekko mózgu bo wiedziałem że potrzebny jest ten kąt by było
90 stopni
i teraz:
90 − (30 −12) −30 = 42

i potem 180−42−102=36

Niby wiedziałem ale nie brnąłem w ten kąt i wszystkie twierdzenia do PT na blache.. Eto chyba
ze masz jakiś fajny plan czego sie uczyć co potwarzac do matury
Plan na dziś:
kończe maturę
https://matematykaszkolna.pl/strona/2585.html to było 8
potem angielski ile dam rade do 23:00
bo jeszcze nic do angielskieog nie potwarzałem

4 maj 21:36
Hugo: Eto jutro tylko 30%

i koniec Polskiego do końca życia
4 maj 21:37
Hugo: licze że posiedzisz tu jeszcze ze mną lece kolejne

4 maj 21:38
Eta:
Ciekawe co powie Twoja mama( polonistka) na te 30%

4 maj 21:40
Hugo: liczby 1,2,3,4,5,6,7,8 ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo że w tym
ustawieniu suma
kazdych dwóch sąsiednich liczb bedzie nieparzystą. Wynik podaj w postaci
ułamka nieskracalnego.
Ω ustawiamy losowo w szeregu czyli 8!

zasada mnożenia

bo na pierwszym miejscu można jedną
z 8 potem na kolejnym jedną z 7 ...
Ω=40320
np.12 34 56 78
czyli parzysta koło nie parzystej
2
4
6
8
te miejsca mogą wariować i potem wszystko razy dwa bo można 8
642_
I znowu zasada mnożenia

?
na pierwszy miejscu można max 4 wsadzić potem 3..2..1.
więc
A= 4! *2=48
4 maj 21:46
Hugo: Eto XD poprzestaje na małym (stoicyzm) .. widzę czytasz moje posty

4 maj 21:46
Hugo: Źle mam bo to jeszcze bedzie wiecej daj sekundke
...2 ...4... 6...8
...2 ... 4 ...6... 8
4 maj 21:48
4 maj 21:49
Hugo: ..2 ...4... 6... 8
I na ile można zamieniać kolejność

to bedzie wariacja bz potwórzeń
4 maj 21:51
Hugo: mietek:
Na maturzę bedzie google boleć wtedy mi też podlinkujesz

?
Ja tu robie LIVE STREAM bo szkoda zeszytu a też licze na integracje
4 maj 21:52
Hugo: To będzie podwójna permutacja
A = 4! * 4! = 24*24= 576
gdyż na 4 silnia mogą sb wędrować nie parzyste i potem na 4 parzyste
1...3...5....7...
..2....4..6....8
| | 576 | | 1 | |
P(A)= |
| = |
| .. dużo skracałem |
| | 40320 | | 70 | |
Dobra pewnie źle .. źle?

4 maj 21:57
mietek: można zacząć też od parzystej...
pnpnpnpn
musisz wynik pomnożyć przez 2
4 maj 22:03
Hugo: dostałbym 3/4 pkt bo nie przemnożyłem razy dwa

4 maj 22:04
Hugo: żałosne zrobić wszystko i wgl i pkt leci −.−"
4 maj 22:05
Hugo: 23:00 − (2 zadanka) = (angielski)

do pracy !
4 maj 22:06
Hugo: Punkt A(2,−3) jest wierzchołkiem rombu ABCD o polu równym 300. Punkt S(3,4) jest środkiem
symetrii tego rombu. Wyznacz wspólrzędne pozostałytch wierzchołków tego rombu.
4 maj 22:07
Hugo:
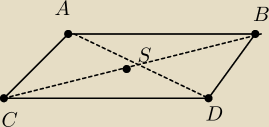
P=300
S(3,4)
A(2,−3)
banalne tyle że bedzie w uj liczenia

4 maj 22:08
Hugo: ... i temu ide na AGH

4 maj 22:09
Hugo: Czy przekątne rombu sie przecinają pod kątem prostym

? .. nie prawda

?
P=0,5 p * q (przekątne p i q) = 300
Prosta
|AS|
S(3,4)
A(2,−3)
y=ax+b
4=3a+b
−3=2a+b /*(−1)
4=3a+b
3=−2a−b
7=a
4=3a+b
4=3*7+b
b=−17
4 maj 22:14
Hugo: prosta
|AS| ma postać
y=7x−17
S(3,4)
A(2,−3)
Liczymy długość |AS|
|AS|=
√(3−2)2 + (4−−3)2
|AS|=
√1 + 49
|AS|= √50
Zatem skoro S jest środkiem |AD| to |SD| =
√50 i ma tę samą prostą...
|AS|=
√50
y=7x−17
√50=
√(3−x)2 + (4−y)2
y=7x−17
√50=
√(3−x)2 + (4−(7x−17))2
√50=
√9+x2−6x + (4−7x+17))2
√50=
√9+x2−6x + (−7x+21))2
√50=
√9+x2−6x + 49x2+441−294x
√50=
√ 50x2+450−300x //bardzo przyjemne równanie

//podnosimy do kwadratu
50= 50x
2+450−300x
0= 50x
2+400−300x /:50
x
2−6x+8=0
Δ=36−32=4
6−2/2 v 6+2/2
x= 2 (odrzucamy bo to z pkt A) v x=4
C(4,y)
y=7x−17
y=28−17=11
C(4,11)
4 maj 22:24
Hugo:
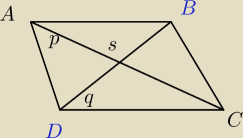 (4, 11)
(4, 11)
wiemy ze pole = 300
300=q*p*0,5
600=p*q
600= 2*
√50*q
q=300 /
√50
q= 6
√50
4 maj 22:28
4 maj 22:30
Hugo: zatem
prosta przechodząca przez |DB| jest prostopadła do y=7x−17 zatem współczynnik a ma odwrócony i
o przeciwnym znaku
podstawiamy pkt S(3,4)
4 maj 22:34
Hugo: q= 6
√50
0,5q=3
√50
S(3,4)
3
√50=
√(x−3)2 + (x−4)2
| | 1 | | 3 | |
3√50= √(x−3)2 + ((− |
| x + 4 |
| )−4)2 |
| | 7 | | 7 | |
| | 1 | | 3 | |
3√50= √(x−3)2 + ((− |
| x + |
| )2 |
| | 7 | | 7 | |
| | 1 | | 9 | | 6x | |
3√50= p{x2−6x+9 + |
| x2 + |
| − |
| //do potęgi 2 |
| | 49 | | 49 | | 7 | |
| | 1 | | 9 | | 6x | |
450= x2−6x+9 + |
| x2 + |
| − |
| |
| | 49 | | 49 | | 7 | |
| | 1 | | 9 | | 6x | |
0= x2−6x−441 + |
| x2 + |
| − |
| /*49 |
| | 49 | | 49 | | 7 | |
49x
2−294x−21609+x
2+9−42x=0
50x
2−336x−21600=0
25x
2−168x−10800=0
ale pewnie i tak by wyszło

4 maj 22:48
Eta:
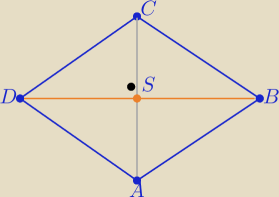
Nieco krócej:
C(2x
S−x
A, 2y
S−y
A)= (4,11)
| | 1 | |
prosta DB ⊥ AC ⇒ aDB=− |
| |
| | aAC | |
| | 1 | |
to: DB: y=− |
| (x−xS)+yS ⇒ DB: x=31−7y to D(31−7y,y) |
| | 7 | |
P(rombu)= 4*P(ΔDCS)=300 ⇒ P(DCS)=75
→ →
P(DCS)=0,5|d(SD, SC)|= 75
→ →
SD=[31−7y−3,y−4] , SC=[1,7]
|(28−7y)*7−1*(y−4)|= 150
dokończ ...... otrzymasz współrzędne punktów D i B
4 maj 22:51
Eta:

4 maj 23:04
Hugo: trzeba iść spać

... a ja jestem w liceum i vektory mnie nie obowiazują.. chyba

4 maj 23:16
Hugo: robilem teraz ciagi...
4 maj 23:16
Eta:
Hej
Mila 
Czemu wykasowałaś swoje rozwiązanie?

4 maj 23:17
Hugo: |(28−7y)*7−1*(y−4)|= 150
|196−49y−y+4|=150
|200−50y|=150
200−50y=150 v 200−50y= − 150
y=1 v y= 7
podstawiamy do prostej

nie mam prostej
musisz mnie tego nauczyc wszystkiego w wakacje

4 maj 23:20
Hugo: Mila siedzi w górach

4 maj 23:20
4 maj 23:22
Mila:
Witam , wróciłam z majówki

4 maj 23:22
Eta:
dla y= 1 D(31−7y,y) =....... dla y=7 B(31−7y,y)=......
4 maj 23:23
Mila:
Dobra prosta .
4 maj 23:23
Eta:
Nie

Huguś ..... dobra prosta

4 maj 23:25
Hugo: | | 3 | | 1 | | 3 | | 1 | |
−3+ |
| =− |
| x v 3+ |
| =− |
| x /*7 |
| | 7 | | 7 | | 7 | | 7 | |
−21+3= −x v 21+3= −x
x=−18 v x=+24
4 maj 23:26
Eta:
No i pięknie .......

4 maj 23:26
Hugo: Hugus

Jeszcze nikt tak mni nie nazwał

4 maj 23:26
Hugo: nie dokońca pięknie xd bo mi wychodzi 18 i −24 (inne znaki) cos sie machłem gdzieś
4 maj 23:27
Eta:
A teraz do
spania , bo jutro
matura 
4 maj 23:27
Hugo: | | 1 | | 3 | |
dla prostej y=+ |
| x+4 |
| by zaszło... ale tak nie mozna |
| | 7 | | 7 | |
4 maj 23:29
Hugo: Eto mam źle .... znajdziesz błąd?
4 maj 23:30
Hugo: −21+3= −x v 21+3= −x
x=18 v x=−24
wychodzi mi 18 i −24 a ma być −18 i 24
4 maj 23:30
Eta:
7y= −x+31 teraz dokończ...... dla y=1 i y= 7
4 maj 23:32
Eta:
| | 3 | | 1 | |
Wpis23:26 −3− |
| = − |
| x ⇒ |
| | 7 | | 7 | |
4 maj 23:36
Eta:
Na przyszłość : nie męcz się z
ułamkami (pomnóż równanie obustronnie przez
7
i po b
ólu

4 maj 23:39
Hugo: 
Hugo wraca z kanapeczką
4 maj 23:40
Eta:

...a ja z herbatką

4 maj 23:41
Hugo: wychodzi

4 maj 23:42
Eta:

4 maj 23:42
Hugo: Eto dowcipasie

Powiedz gdzie mam iść na studia żeby Cię spotkać
4 maj 23:42
Hugo: już bez tej ironi.. Hugo sie myli ale generalnie sb radzi

4 maj 23:43
Eta:
Ja jestem dopiero w ILO

4 maj 23:43
Hugo: Gdzieś blisko Oświęcimia : P ? Bym wpadł odwiedził !
4 maj 23:44
Hugo: A jak sie moge spytać; Olimpiady czy coś? Jestes prze mądra

!
4 maj 23:44
Eta:
Hugusiu

... błagam idź już do

Miłych snów , powodzenia jutro i napisz na 60% j.polski

4 maj 23:47
Hugo: Tak ci powiem ... że jak robie sb te matury... To każde zadanie rozumiem (czasem mi brakuje
wzoru lub zależności) ... To się dowkuwa do PT i generalnie z odrobiną szczęscia jak bym sie
nie machnął nigdzie z uwagi na nie staranność pisma i tego xd To
Istnieje takie p dla którego argumenty zbioru MAtURY HUGA przyjmują wartości 100% na maturze

Jak mnie oceniasz 70? .. zrozumiem

Poza tym żeby sie dostać na AGH chce zadziwić moją matematyczke
4 maj 23:48
Hugo: 30%

!
buzi na dobranoc bo Hugo po kawie nie zaśnie

4 maj 23:48
lisek: bzdura

nic nie umiecie
5 maj 08:38
 odcinek CD jest zawart w dwusiecznej kąta ACB trójkąta ABC kąty trójkąta ABC mają miary
|CAB|=42, |ABC|=78 Styczna do okręgu opisana na tym trójkącie w punkcie C przecina prostą AB w
punkcie E. Oblicz ile stopni ma każdy z trójkątów CDE
odcinek CD jest zawart w dwusiecznej kąta ACB trójkąta ABC kąty trójkąta ABC mają miary
|CAB|=42, |ABC|=78 Styczna do okręgu opisana na tym trójkącie w punkcie C przecina prostą AB w
punkcie E. Oblicz ile stopni ma każdy z trójkątów CDE

 Skoro |CD| to dwusieczna to dzieli na dwa równe kąty czyli |ACD|=|DCB|=α
Trójkąty ACD i tr. CBD
ACD = 42+ α + β
CBD = 78+ α + 180−β
Trójkąt ABC = 180 = 42+72+x
x=66
α=33
tr. ACD
180−33−42=105
kąt. |CDB| = 180−105=75
kąt |CBE|
180−28=102
Skoro |CD| to dwusieczna to dzieli na dwa równe kąty czyli |ACD|=|DCB|=α
Trójkąty ACD i tr. CBD
ACD = 42+ α + β
CBD = 78+ α + 180−β
Trójkąt ABC = 180 = 42+72+x
x=66
α=33
tr. ACD
180−33−42=105
kąt. |CDB| = 180−105=75
kąt |CBE|
180−28=102
 Trzy trójkąty: 3 równania
dwie nie wiadoome bo jeden mamy juz policzony=75
Trzy trójkąty: 3 równania
dwie nie wiadoome bo jeden mamy juz policzony=75

 bo już nawet nie wiesz,że 180−(42+78)= ?
bo już nawet nie wiesz,że 180−(42+78)= ?
 Eto zepsułaś zabawe
Eto zepsułaś zabawe Tego mi brakowało że 78 razy dwa to kąt ten drugi czerwony
Tego mi brakowało że 78 razy dwa to kąt ten drugi czerwony  Ale doznałem prania lekko mózgu bo wiedziałem że potrzebny jest ten kąt by było 90 stopni
i teraz:
90 − (30 −12) −30 = 42
Ale doznałem prania lekko mózgu bo wiedziałem że potrzebny jest ten kąt by było 90 stopni
i teraz:
90 − (30 −12) −30 = 42  i potem 180−42−102=36
i potem 180−42−102=36  Niby wiedziałem ale nie brnąłem w ten kąt i wszystkie twierdzenia do PT na blache.. Eto chyba
ze masz jakiś fajny plan czego sie uczyć co potwarzac do matury
Plan na dziś:
kończe maturę https://matematykaszkolna.pl/strona/2585.html to było 8
potem angielski ile dam rade do 23:00
bo jeszcze nic do angielskieog nie potwarzałem
Niby wiedziałem ale nie brnąłem w ten kąt i wszystkie twierdzenia do PT na blache.. Eto chyba
ze masz jakiś fajny plan czego sie uczyć co potwarzac do matury
Plan na dziś:
kończe maturę https://matematykaszkolna.pl/strona/2585.html to było 8
potem angielski ile dam rade do 23:00
bo jeszcze nic do angielskieog nie potwarzałem 
 i koniec Polskiego do końca życia
i koniec Polskiego do końca życia


 zasada mnożenia
zasada mnożenia  bo na pierwszym miejscu można jedną
z 8 potem na kolejnym jedną z 7 ...
Ω=40320
np.12 34 56 78
czyli parzysta koło nie parzystej
2 4 68
te miejsca mogą wariować i potem wszystko razy dwa bo można 8642_
I znowu zasada mnożenia
bo na pierwszym miejscu można jedną
z 8 potem na kolejnym jedną z 7 ...
Ω=40320
np.12 34 56 78
czyli parzysta koło nie parzystej
2 4 68
te miejsca mogą wariować i potem wszystko razy dwa bo można 8642_
I znowu zasada mnożenia  ?
na pierwszy miejscu można max 4 wsadzić potem 3..2..1.
więc
A= 4! *2=48
?
na pierwszy miejscu można max 4 wsadzić potem 3..2..1.
więc
A= 4! *2=48


 to bedzie wariacja bz potwórzeń
to bedzie wariacja bz potwórzeń
 ?
Ja tu robie LIVE STREAM bo szkoda zeszytu a też licze na integracje
?
Ja tu robie LIVE STREAM bo szkoda zeszytu a też licze na integracje


 do pracy !
do pracy !
 P=300
S(3,4)
A(2,−3)
banalne tyle że bedzie w uj liczenia
P=300
S(3,4)
A(2,−3)
banalne tyle że bedzie w uj liczenia 

 ? .. nie prawda
? .. nie prawda  ?
P=0,5 p * q (przekątne p i q) = 300
Prosta
|AS|
S(3,4)
A(2,−3)
y=ax+b
4=3a+b
−3=2a+b /*(−1)
4=3a+b
3=−2a−b
7=a
4=3a+b
4=3*7+b
b=−17
?
P=0,5 p * q (przekątne p i q) = 300
Prosta
|AS|
S(3,4)
A(2,−3)
y=ax+b
4=3a+b
−3=2a+b /*(−1)
4=3a+b
3=−2a−b
7=a
4=3a+b
4=3*7+b
b=−17
 //podnosimy do kwadratu
50= 50x2+450−300x
0= 50x2+400−300x /:50
x2−6x+8=0
Δ=36−32=4
6−2/2 v 6+2/2
x= 2 (odrzucamy bo to z pkt A) v x=4
C(4,y)
y=7x−17
y=28−17=11
C(4,11)
//podnosimy do kwadratu
50= 50x2+450−300x
0= 50x2+400−300x /:50
x2−6x+8=0
Δ=36−32=4
6−2/2 v 6+2/2
x= 2 (odrzucamy bo to z pkt A) v x=4
C(4,y)
y=7x−17
y=28−17=11
C(4,11)
 (4, 11)
wiemy ze pole = 300
300=q*p*0,5
600=p*q
600= 2*√50*q
q=300 / √50
(4, 11)
wiemy ze pole = 300
300=q*p*0,5
600=p*q
600= 2*√50*q
q=300 / √50

 Nieco krócej:
C(2xS−xA, 2yS−yA)= (4,11)
Nieco krócej:
C(2xS−xA, 2yS−yA)= (4,11)

 ... a ja jestem w liceum i vektory mnie nie obowiazują.. chyba
... a ja jestem w liceum i vektory mnie nie obowiazują.. chyba 
 Czemu wykasowałaś swoje rozwiązanie?
Czemu wykasowałaś swoje rozwiązanie? 
 nie mam prostej
musisz mnie tego nauczyc wszystkiego w wakacje
nie mam prostej
musisz mnie tego nauczyc wszystkiego w wakacje 


 Huguś ..... dobra prosta
Huguś ..... dobra prosta 

 Jeszcze nikt tak mni nie nazwał
Jeszcze nikt tak mni nie nazwał 


 Hugo wraca z kanapeczką
Hugo wraca z kanapeczką
 ...a ja z herbatką
...a ja z herbatką 


 Powiedz gdzie mam iść na studia żeby Cię spotkać
Powiedz gdzie mam iść na studia żeby Cię spotkać


 !
!
 ... błagam idź już do
... błagam idź już do  Miłych snów , powodzenia jutro i napisz na 60% j.polski
Miłych snów , powodzenia jutro i napisz na 60% j.polski

 Jak mnie oceniasz 70? .. zrozumiem
Jak mnie oceniasz 70? .. zrozumiem  Poza tym żeby sie dostać na AGH chce zadziwić moją matematyczke
Poza tym żeby sie dostać na AGH chce zadziwić moją matematyczke
 !
buzi na dobranoc bo Hugo po kawie nie zaśnie
!
buzi na dobranoc bo Hugo po kawie nie zaśnie
 nic nie umiecie
nic nie umiecie