matura zawodus: Matura to bzdura Zadanie 1 (4pkt) Rozwiąż nierówność |x−1|+|x²−4|≥x+4 Zadanie 2 (5pkt) Wyznacz wszystkie wartości parametru m, dla których pierwiastki rzeczywiste równania (m+1)x²+14x+6m²+8 spełniają warunek x₁<m<x₂ Zadanie 3 (3 pkt) Wykaż, że dla dowolnych liczb rzeczywistych a i b prawdziwa jest nierówność a(a+2b)≥(6−3b)b−17 Zadanie 4 (4 pkt) Dany jest trójkąt ABC o podstawie AB. Wysokość CD poprowadzona z wierzchołka C dzieli podstawę na dwa odcinki takie, że |AD|=72 cm i |DB|=28 cm. Prostopadle do podstawy poprowadzono prostą, która podzieliła trójkąt ABC na dwa trójkąty o równych polach. Oblicz długość odcinków na które ta prosta podzieliła podstawę trójkąta ABC. Zadanie 5 (4 pkt) Wyznacz wszystkie liczby naturalne a i b dla których pierwiastkiem wielomianu

	ab		11
W(x)=x3+(		−b)x2−(a+		)x+2 jest liczba pierwsza.
	4		2

Zadanie 6 (4 pkt) Dany jest okrąg o równaniu x²+y²+6x−4y−5=0. Wyznacz miarę kąta utworzonego przez dwa promienie poprowadzone do punktów przecięcia się tego okręgu z osią OY Zadanie 7 (4 pkt) Rozwiąż równanie

	1
		cosx+ 2sin2x = 1+sin2xcosx
	2

w przedziale <0,2π> Zadanie 8 (4 pkt) Oblicz ile jest liczb naturalnych 10 cyfrowych, których suma cyfr wynosi co najmniej 4. Zadanie 9 (4 pkt) Dany jest sześcian ABCDA₁B₁C₁D₁ o podstawach ABCD i A₁B₁C₁D₁. Przez przekątną AC podstawy i środki krawędzi A₁D₁ i C₁D₁ poprowadzono płaszczyznę. Wykaż, że przekątne otrzymanego przekroju przecinają się pod kątem 90 stopni. Zadanie 10 (5 pkt) Ciąg liczbowy (x,y,z) jest rosnącym ciągiem geometrycznym i x+y+z=42, natomiast ciąg

	z
(x+4,y−4,		) jest arytmetyczny. Oblicz x,y,z.
	16

Zadanie 11 (6 pkt) W urnie znajdowało się 10 kul białych i n kul czarnych. Z urny wylosowano dwa razy po jednej kuli bez zwracania. Oblicz ile było kul w urnie jeśli prawdopodobieństwo wylosowania kul

	35
różnego koloru jest większe od		.
	68

Zadanie 12 (3 pkt)

	1
Dana jest funkcja f(x)=
	x−1

a) narysuj wykres funkcji g(x)=|f(|x|)| b) Podaj wszystkie wartości parametru m, dla których równanie g(x)=m ma dokładnie 3 rozwiązania.

Marcin: Dziękuję ślicznie W sam raz na nockę ta maturka

Saizou : mogę się dołączyć xd?

zawodus: Mam nadzieję, że wszystko dobrze przepisałem z kartek i nie ma żadnych literówek Jestem ciekaw jak oceniacie poziom trudności zadań

zawodus: Saizou nigdzie nie ma napisane, że nie wolno się dołączyć Proszę tylko "ekspertów" o nie zepsucie zabawy

Marcin: Mamy tutaj pisać odpowiedzi do sprawdzenia?

Saizou : to zadanie 5 jest takie proste czy mi się wydaje ?

muflon: To są przecieki z CKE?

zawodus: To zależy tylko od was Można się umówić na podanie odpowiedzi jak wszyscy wszystko zrobią tutaj inwencja leży po waszej stronie

zawodus: Saizou jeśli dla ciebie jest proste to nie musi być proste dla wszystkich Dla osób, które mają wyniki około 90% to wszystko jest proste Tak oficjalne przecieki

Saizou : mi w sumie obojętnie

Marcin: Tam chyba jedynym możliwym pierwiastkiem (liczbą pierwszą), jest 2, tak? W piątym.

ułan: dobry wałek z tymi przeciekami

kyrtap: Macie mi nie podawać odp do rana tutaj

kyrtap: bo uduszę

Marcin: heheh to groźba czy prośba?

kyrtap: tym razem groźba

kyrtap: ps Marcin że tak wyrażę prostacka ta matura z sierpnia

Saizou : no to w pierwszym wyszedł przedział x∊.....

Marcin: Skoro prostacka, to chyba dobrze

kyrtap: Saizou spróbuj

kyrtap: zawodus a sam policzyłeś to?

kyrtap:

zawodus: mam wszystkie odpowiedzi, bo 9 zadań jest czysto autorskich jedno ze zmienionymi danymi a dwa przepisane. Niestety, ale zadań z geometrii tak szybko się nie wymyśla

kyrtap: dziękuje bardzo za przygotowanie zadań

kyrtap: Marcin od której to maturę byś robił bo ja z jakieś 45 minut bym odpoczął

Saizou : zawodus powiem ci że poziom taki średni xd taka może być w maju

kyrtap: Saizou to ty będziesz mieć chyba 100 % w maju?

kyrtap: ale zgodzę Saizou że ta matura w porównaniu z tymi z Pazdro jest trochę łatwiejsza

Saizou : chyba nie

Marcin: Ja też na razie odpoczywam kyrtap Saizou z tym 5 miałbym chyba problem. Będą takie dwie pary liczb? Czy coś mieszam?

zawodus:

zawodus: to nie miała być odpowiedź Marcin dla ciebie

Marcin: Jaka odpowiedź? Jak ja tu żadnej odpowiedzi nie widzę

ułan: w drugim zadaniu warunek Δ>0. nie da się tego policzyć wychodzi wielomian 3 stopnia z którego się rozwiacać nie da

zawodus: idę na film Powodzenia wszystkim, którzy rozwiązują te zadanka

zombi: Nie rzucajcie na razie rozwiązań pls. Może umówimy się na konkretną godzinę i wtedy zawodus od razu wszelkie wątpliwości rozwieje. No chyba, że bardzo wam zależy wrzucać je już teraz, to nie ma problemu.

Marcin: Ja jestem na tam (jeżeli chodzi o propozycję zombi) Odpowiedzi będę o 5 rano, ok?

Marcin: na tak*

kyrtap: weźcie nie komentujcie narazie tej matury tylko przysiądźcie do niej i zróbcie ją w spokoju bo tak to co to za robota

kyrtap: ja podam swoje o 3 w nocy

Marcin: Jak ja jej teraz nie robię!

zawodus: tak i ja wstanę o 5 rano żebyście mnie czasem tutaj nie ujrzeli o tej godzinie

Marcin: A po co masz iść spać?

kyrtap: Marcin przez Ciebie się tylko przestawiłem ze spaniem

zawodus: Ja w przeciwieństwie do was jestem człowiekiem i muszę spać

Marcin: głupoty gadasz

kyrtap: a my to co jakieś grzyby?

Marcin: Nadludź. Ty jesteś kyrtap nadludź

kyrtap: czemu ja ?

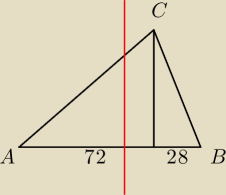
razor: Chyba nie do końca rozumiem zadanie 4. Jeżeli podzielimy trójkąt ABC prostą prostopadłą do podstawy to powstanie trójkąt i czworokąt a nie dwa trójkąty?

Marcin: Bo tak mocno ogarniasz matmę

kyrtap: hahaha teraz to mnie rozśmieszyłeś ja i ogarnianie matmy

kyrtap: razor wszystko się wyjaśni o 5 rano narazie sam pomyśl

Saizou : pytanie do Marcina kto wprowadził koncepcję nadczłowieka ?

zawodus: UWAGA UWAGA W zadaniu 4 powinno oczywiście być ... podzieliła trójkąt ABC na dwie figury o równych polach. Bardzo przepraszam za błąd w przepisywaniu

Marcin: Saizou, chodzi Ci o Hitlera?

Saizou : nie....

Saizou : ale z narodowością trafiłeś

Marcin: a to luzik

52: Ktoś z Młodej Polski ?

Marcin: Przykro mi, nie wiem

5-latek: chyba to byl niczego sobie (ten ktory wymyslil

kyrtap: na zasadzie eliminacji wybiorę 7 streszczeń do przeczytania

Saizou : właśnie też tak myślałem, ale potem sprawdziłem i się okazało że wprowadził to rusek

Saizou : no to też zależy gdzie wprowadził xd − do literatury − do filozofii

Marcin: To dopisz na wikipedii, że wprowadziłem koncepcję nadczłowieka na stronę matematyka.pisz.pl

Saizou : haha, widzę że już sprawdziłeś xd

Marcin:

bezendu: Witam Ej nawet ja bym chyba zrobił wszystkie zadania

kyrtap: to zrób

Marcin: Ja bym chyba 4 nie zrobił. Nie wiem czego się tu zaczepić Ale w sumie dłużej się nie zastanawiałem

kyrtap: A ja jeszcze tego nie robiłem i jadę na pizzę sobie więc do później (trzeba się odstresować)

Domel: razor − ty to niczym Ojciec Mateusz jesteś − każdą pułapkę wykryjesz

kyrtap: Marcin jesteś?

Marcin: Jestem, ale oglądam 'Wesele'

Eta: Czyje?

Marcin: Wyspiańskiego

jakubs: Marcin szybki jesteś Ja dopiero będę czytał Nie Boską komedię

kyrtap: serio Ci się chce to oglądać nie lepiej streszczenia poczytać?

kyrtap: ja jutro lektury zaczynam

kyrtap: teraz się biorę za arcy ciekawą maturę stworzoną przez zawodusia

Marcin: Nie, nie chce mi się! Niestety bardziej wpada mi do głowy film, niż przeczytane streszczenie. Nie−boska komedia jest poryta

Marcin: Powiedz jaki masz wynik w prawdopodobieństwie, bo jestem ciekawy czy mi się zgadza

kyrtap: dopiero wróciłem Marcin z pizzy teraz zaczynam ją robić

kyrtap: kilka piw i można robić

Marcin: Kilka piw mówisz? No na trzeźwo robić matury nie wypada

razor: mi wyszło {18,19,20,21,22}

Marcin: W prawdopodobieństwie?

kyrtap: Cicho z tymi odpowiedziami

kyrtap: cisza nocna

Marcin: No tak razor, poryłem się Mam to samo, dzięki

razor: a 2 zrobiłeś? jakieś kosmiczne rzeczy mi wychodzą przy Δ

kyrtap: cisza nocna

Marcin: https://www.wolframalpha.com/input/?i=14%5E2-+4%28m%2B1%29%286m%5E2%2B8%29%3E%3D0 Zawodus pewnie źle przepisał

Hugo: Hugo s.ie kompíe ale chetnie zazyje z wamí troche org** btw 20min

kyrtap: spoko Hugo

Marcin: To kto pisze za Hugo skoro on się kąpie?

kyrtap: mama?

Marcin: Pewnie tak Ciekawe czy zrobisz 4, bo ja nie mam pomysłu

kyrtap: z piwem zawsze zrobię

Hugo: asystetka

Piotr: w zad 2 to w ogole nie ma rownania

kyrtap: no chciałem to napisać bo nie ma równa się zero

kyrtap: ale mniejsza z tym

Marcin: Czepiacie się

Piotr: a skad wiesz, ze jest = 0 ?

kyrtap: Piotr tak na marginesie napisał

kyrtap: no nie wiem przykładowo napisałem zazwyczaj tego typu równania kończą się zerem

Hugo: co sadzicie o ty ze oke robi w 1dniu mature z ang P i R? rok temu bylo tak z matma

Marcin: Ja się z tego cieszę. Przynajmniej nie muszę dwa razy jechać do szkoły

kyrtap: delta w drugim się zeruje?

kyrtap: znaczy te wyrażenie z delty?

Marcin: Nie. Chociaż nie do końca rozumiem o co pytasz

kyrtap: bo warunek musi być Δ>0 i tam pod deltą stoi wyrażenie m i coś nie widzę pierwiastków tej nierównośći

Piotr: nie. przeciez Marcin dal link co wychodzi z delty. zawodus gdzies walnal byka. i dlatego niewiadomo, gdzie i co jest po =.

kyrtap: aha luz czyli to zadanie z błędem oki

Marcin: Ty się nie kapnąłeś że jest błąd?

kyrtap: nie nie zwróciłem uwagi ale tak przeczuwałem że coś nie tak

Marcin: http://pl.memgenerator.pl/mem-image/przed-matura-spijam-tylko-wiedze-pl-ffffff 4you kyrtap

kyrtap: Marcin trzeba też odreagować

Marcin: No tak. I przed i po

kyrtap: ja Marcin potrzebuję też tego bo jak podejdę spięty do tego najważniejszego egzaminu to będą nici

razor: ktoś zrobił 4?

Marcin: Nie ma się co spinać Ja się ewentualnie zepnę przed polskim

Marcin: Ja nie zrobiłem. Nie mam pomysłu właśnie na to 4.. razor, dałeś radę?

kyrtap: ludziki jak napisałem (a+b)² +(b−2)² + (b−1)² +12≥0 to już wykazałem nie?

razor: kyrtap tak Marcin zrobiłem ale nie wiem czy dobrze mogę wrzucić jeśli chcesz

kyrtap: nie jeszcze razor

kyrtap: ja pomyślę

Marcin: (a+b)² + (4b²−6b+17) ≥ 0 Według mnie, to nawet coś takiego wystarczy.

razor: no ale wypadałoby napisać co oznacza wtedy Δ < 0

kyrtap: według mnie to nie starcza mi

Marcin: No tak, ale chodzi mi o sam zapis końcówki. Wiadomo, że później jeszcze liczysz Δ, która jest ujemna

kyrtap: dla Marcina to jeszcze przed przekształceniami było to oczywiste

kyrtap:

zombi: Ktoś 4, bo nie wiem czy takie śmieszne rzeczy mają wychodzić ?

Marcin: Tam ma być 2b², a nie 4b², bo się znowu walnąłem przy przepisywaniu No kyrtap powiedzi mi, że pokazanie że Δ<0 nie oznacza prawdziwości tej nierówności dla każdej liczby rzeczywistej

kyrtap: czekajcie tu mi się nasuwa jakieś twierdzonko one moment

Marcin: Zombi, pogadaj z razorem

razor: zombi zrobiłem, ile ci wyszło?

kyrtap: wiem wiem ale dla ciebie ta nierówność jest już oczywista a(a+2b)≥(6−3b)b−17

Marcin: Wiadomo że jest oczywista Ja to widzę, ale muszę to tym gościom z CKE udowodnić, bo nie kumają:(

Marcin: Ja czekam na wasze rozwiązanie zadania 4, bo jestem bardzo ciekawy..

kyrtap: a ja mam pomysł Marcinie

Marcin: To pisz rozwiązanie

kyrtap: muszę dokończyć ale jeszcze nie wiem czy sposób ok

Marcin: To czekam

zombi: Mów pierwszy jak potwierdzę albo zaneguję, bo wstydzę się takich brzydkich liczb wrzucać, bo nie wiem czy to jest ok.

razor: moje liczby raczej brzydkie nie są 60 i 40

kyrtap: poczekajcie bo ja nie jestem ekspertem w geometrii

Marcin: O prosze jaki ładny wynik

kyrtap: jednak mój sposób dał plamę ale nie dawajcie jeszcze rozwiązania

zombi: Czekaj, jeszcze raz policzę, może mam w rachunkach błąd. z/w

kyrtap: idę spać bo zasnąłem przy kompie zrobię jutro te zadanka na kozaku

Marcin: Widzę że u Ciebie jest coraz gorsza forma ze snem

zombi: Dobrze razor tez mam 60 i 40. Błąd w rachunkach miałem.

Marcin: zad 1: x∊(−∞; √2−1> ∪ <3;+∞)

Marcin: Zombi, ew. Razor. Możecie napisać rozwiązanie tego zadania?

razor: Marcin zgadza się

razor: Mogę wrzucić swoje

Marcin: Dziękii

zombi: Tak w pierwszym mam to samo.

zombi: 8 przez zaprzeczenie, ale wynik jaki macie?

Marcin: W sumie nie liczyłem. Ale też robiłbym przez zaprzeczenie

razor:

	1
P ΔABC =		100h = 50h
	2

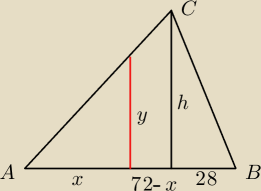
	h		y
z tw. Talesa −		=		⇒ 72y = hx
	72		x

Czerwona kreska dzieli ten trójkąt na dwie figury o tym samym polu

1
	xy = 25h
2

Druga figura to połączenie trapeza prostokątnego o podstawach h, y i wysokości 72−x oraz trójkąta prostokątnego o bokach 28 i h

1		h+y
	28h +		(72−x) = 25h
2		2

Rozwiązując ten układ równań mamy x = 60

kyrtap: mogę przedstawić swój sposób bo inaczej wyliczyłem przed zaśnięciem

razor: w 4 mam 9*10⁹ − 67

zombi: Troszkę szybciej mam:

x		h
	=		⇔72y = hx
y		72

oraz xy = 50h czyli xy=50h hx=72y dzielę stronami, bo można dostaję

	6
72y2 = 50h2 ⇔ h =		y
	5

I podstawiam do xy=50h i mam

	6
xy = 50		y ⇔ y(x−60) =0 ⇔ x=60 nie potrzeba trzeciego równania tutaj.
	5

kyrtap: ja w ogóle inaczej to wyliczyłem ale chyba mój dłuższy sposób

razor: hmm w sumie patrzę na swoje obliczenia i w ogóle z tego 3 równania nie korzystałem

Marcin: Ja mam 66 hmm.. poszukam jeszcze jednej

zombi: Ja mam 9*10⁹ − 66

kyrtap: ja robiłem z tangensa, potem z układu równań

zombi: Też właśnie się zastanawiałem czy potrzebuję to trzecie równanko, ale w sumie to po co sobie utrudniać, życie i spróbowałem z dwoma

razor: Nie szukaj źle spojrzałem powinno być 66

Marcin: Ok, czyli to w sumie przyjemne zadanko było

Marcin: W piątym macie: a=5 b=11 a=7 b=5? Bo nie wiem czy tutaj nie poryłem

zombi: Tak.

Marcin: ok

zombi: i jeszcze a=13 b=3

razor: ja mam jeszcze 13 i 3

Marcin: hehe ok zawsze czegoś nie uwzględnię

zombi: Analityczna kąt 90^o?

razor: tak

Marcin:

	9
No faktycznie, bo mamy przecież b=2+		.. żebym tylko takich błędów za kilka dni nie
	a−4

robił

zombi: Spokojnie Marcin, wchodzisz do sali i jest full skupienie, poza tym masz 3 godziny! W tym czasie możesz spokojnie jeszcze 3−4 razy sprawdzić calutką pracę.

Marcin: 3 godziny to strasznie długo. Ja tak średnio to maturkę w niecałą godzinę robię

razor: Ja tak mam jakoś, że w domu robię więcej głupich błędów niż gdzieś na sprawdzianie czy próbnej maturze

zombi: Ja mam na odwrót na sprawdzian i konkursach i wypalam, a jak robię na spokojnie w domu to wszystko wychodzi. 3 godziny to mega dużo czasu, jeśli zadania będą nad wyraz schematyczne, z automatu, to zamierzam sprawdzić je z 4−5 razy, bo przy takich zadaniach w 1h 20min się kończy pisanie, przynajmniej u mnie.

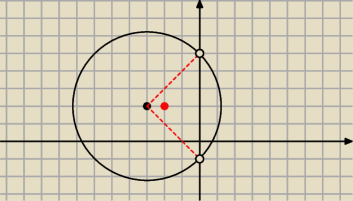
Marcin: Nieźle, ja mam wręcz przeciwnie Analityczna trudna nie była

Marcin: Na pewno będą nad wyraz schematyczne.

zombi: Matura z ubiegłego roku, jeezu gdybyśmy taką dostali to 100% to jest lajcik straszny.

razor: Przez całe liceum miałem sprawdziany robione tak, że jak wiedziało się wszystko to ledwo udawało się zdążyć napisać cały Więc jak raz napisałeś to nie miałeś czasu sprawdzić, trzeba było uważać co się pisze

Marcin: razor, na Ciebie stres działa mobilizująco

Marcin: Dwa lata temu też jakaś specjalnie trudna nie była maturka A CKE daje coraz łatwiejsze.

zombi: Chyba, że nam jako ostatnim ze starą maturą dowalą hardkora

Marcin: Ktoś tu dzisiaj napisał, że dla kogoś kto ogarnia dobrze matmę, to im trudniejsza matura, tym lepiej

zombi: Nie dzisiaj, ostatnio to pisałem.

razor: Spodziewam się jakiegoś ciekawego dowodu na odsiew

Marcin: Co masz na myśli pisząc 'odsiew'?

zombi: No wiesz, żeby oddzielić przeciętnych od mocniejszych. Najlepiej, żeby był algebraiczny Nierówność byłaby

Marcin: Jednym zadaniem różnicy nie zrobisz I powiedzmy sobie szczerze, że 100% to nie tylko wiedza, ale też i szczęście

zombi: Szczęście, dyspozycja dnia. Trzeba próbować + robisz tych zadań tyle właśnie po to, aby się nie mylić na maturze, a jak wiadomo nauka w las nie idzie.

Marcin: Niby nie, ale szkoda mi osób, które wiedzą bardzo dużo, a nie potrafią zdać dobrze matury przez stres..

zombi: Ja idę spać. Trzymajcie się

Marcin: Dobrej nocy zombi

Janek: Rozwiązanie rzekomego przecieku maturalnego https://www.youtube.com/watch?v=wzCOxHTpk8A

zawodus: Kto uważa, że zadania drugiego nie da się rozwiązać?

52: Ja

zawodus: oczywiście Piotrek brakuje =0

zawodus: (w zadaniu 2 powinno być =0), abyśmy mieli równanie To mamy jedną osobę czekamy dalej

asap: Ja też uważam, że nie da się tego zrobić

jerey: zawodus wrzucisz wyniki do zadan?

ułan: #kyrtap jesteś pewny swojego rozwiązania zadania trzeciego?

ułan: ok, jesteś pewny, to ja źle popatrzyłem, sorki

Saizou : można też tak a(a+2b)≥(6−3b)b−17 a²+2ab≥6b−3b²−17 a²+2ab+3b²−6b+17≥0 a²+2ab+b²+b²−6b+9+b²+8≥0 (a+b)²+(b−3)²+b²+8≥0

zawodus: Dobrze zaraz wrzucę wyniki. Część zadań została już poprawnie rozwiązana

zawodus: Saizou umiesz zrobić zadanie 2?

Saizou : szczerze nie rozwiązywałem, wiec daj mi chwilkę

Saizou : x₁<m m<x₁ ======+ x₁−x₂<0 lx₁−x₂l<0 dobrze myślę ?

zawodus: Bo dużo osób twierdzi, że zadania nie da się rozwiązać (dopisz sobie =0, aby mieć równanie)

Saizou : tam powinno być x₁<m m<x₂

zawodus: wg mnie |x₁−x₂|<0 nigdy nie zachodzi

Saizou : xd

zawodus: poza tym, to podobno jest problem z deltą

Piotr 10: A te zadanie 2 można tak? 1⁰ Δ > 0 2⁰ (m+1)*f(m) < 0 3⁰ m+1≠0 ?

Saizou : Δ>0 po przekształceniach 6m³+6m²+8m−41<0

zawodus: Piotrek można, ale nie policzysz delty

Piotr 10: jak to ?

zawodus: umiesz rozwiązać nierówność 6m³+6m²+8m−41>0 ?

Piotr 10: Aaa.. ok .

Piotr 10: Wykaż, że dla dowolnych liczb rzeczywistych a i b prawdziwa jest nierówność a(a+2b)≥(6−3b)b−17 a²+2ab ≥ 6b − 3b² − 17 a²+2ab − 6b+ 3b²+ 17 ≥ 0 a²+2ab + b²+b² − 6b+b²+ 17≥0 (a+b)² +(b−3)²+ b²+8≥0

Saizou : Piotrze dokładnie to samo napisałem o 11:16

Piotr 10: Hehe xD. Ta sama myśl

Piotr 10: Zad 5/ W(2)=0

Saizou : tak

zawodus: Oficjalne odpowiedzi Zadanie 1 x∊(−∞,√2−1> ∪ <3,+∞) − prawidłowa odpowiedź padła wcześniej (ciekawe czy z wolframa czy liczyliście ) Zadanie 2 m∊(−4,−2) Zadanie 3 dowód (jak będą chętni to podam moją wzorcówkę inną od wszystkich ) Zadanie 4 Odcinki to 60 i 40 Zadanie 5 a=5, b=11 lub a=7,b=5 lub a=13,b=3 tutaj też się udało Zadanie 6 kat ma 90 stopni też wyszło (pamiętajcie, że rysunek nie będzie brany jako dowód ) Zadanie 7

	π		3π		5π		7π
x∊{		,		,		,		}
	4		4		4		4

(nikomu się chyba liczyć nie chciało ) Zadanie 8 9*10⁹−66 (to poszło ) Zadanie 9 dowód Zadanie 10 x=2,y=8,z=32 (znów nikt nie ruszył) Zadanie 11 k∊{18,19,20,21,22} (chyba ktoś podał prawidłową odpowiedź) Zadanie 12 a) rysunek można wykonać na stronie www.desmos.com/calculator b) m=1 (znowu nikt nie ruszył) Jak macie pytania lub uwagi to czekam

stefan: możesz przedstawić rozwiązanie zadania drugiego?

zawodus: aż takie trudne było?

panan: może ktoś podać rozwiazanie 5, tutaj coś trzeba kombinować z p. wymiernymi?

zawodus: Jadę na zakupy może ktoś jeszcze wymyśli zadanie 2 Zadanie 5 może ktoś podać rozwiązanie kto zrobił (a tacy byli)

razor: zgadza mi sie wszystko ale tego 2 bym nie zrobil raczej, nawet gdyby delta wychodzila normalnie

jerey: w zadaniu 4. poprowadzono prostą prostopadłą do AB ktora podzieliła na 2 trojkąty o równych polach. ? nie bardzo rozumiem ? wychodzi na to ze podzieliła na trójkąt i czworokąt ?

stefan: była poprawka, chodzi o dwie figury o takich samych polach

jerey: własnie zauwazyłem przed chwilką

kyrtap: Zadanie z analityczną można rozwiązywać z rysunku ?

razor: nie

kyrtap: oki

kyrtap: czyli nie mogę brać punktów przecięcia osi oy z okręgiem

kyrtap: ?

Saizou : możesz, ale musisz je policzyć a nie z rysunku odczytać

kyrtap: dobra już chyba mam pomysł ale nie powiem w tym wypadku rysunek dużo pomaga

zawodus: Rysunek to podstawa Co z zadaniem drugim?

kyrtap: już potem można np z tw. cosinusów pojechać?

kyrtap: będę myślał bo mam chyba koncepcję

kyrtap: zawodus z cosinusów można obliczyć gdy jest analityczna?

Karol: Teraz by było super, jakby ktoś podał sposób rozwiązania wszystkich zadań !

Saizou : zawodus wolfram podaje że

	1		1		389
−6(m+		)3−6(m+		)+		>0
	3		3		9

	389
−6t3−6t+		>0
	9

54t³−54t+389>0

zawodus: Kyrtap można ale najlepszy sposób to iloczyn skalarny. Saizou tej nierówności z delty nie umiecie rozwiązać. Trzeba to zrobić inaczej

kyrtap: nie miałem iloczynu skalarnego

kyrtap: zawodus ze wzorów Vietea dla pierwiastka 3 stpopnia?

kyrtap: czy się mylę ?

Piotr 10: Ktore zadanie ?

jerey: równanko trygonom. bardzo przyjemne

kyrtap: jerey każde równanko trygonometryczne jest przyjemne

kyrtap: Piotrze w drugim

Piotr 10: A chodzi Ci o rozwiązanie tej nierownosci ?

kyrtap: tak

Piotr 10: To daj sobie spokój

kyrtap: czemu?

kyrtap: za trudne dla mnie ? czy jak?

Piotr 10: Bo jak zawodus powiedział, my jej nie rozwiazemy

zombi: A tam gadasz Piotrze http://www.math.us.edu.pl/pgladki/faq/node127.html

Piotr 10: No i masz . zombi fajne wzorki

zombi: Kiedyś liczyłem sobie takie pierwiastki dla śmiesznych wielomianów, nie polecam

kyrtap: aha spoko Piotrze

kyrtap: robiliście zadanie z ciągiem z układu równań?

Piotr 10: Ja nie robiłem

razor: robiłem

zombi: ja też

Marcin: Ja narysowałem tylko taki poglądowy rysunek do analitycznej. Przecież wiem, że muszę jeszcze dodać obliczenia

kyrtap: w omedze będzie C²_n+10?

jerey: własnie , zrobił ktos 11? mi cos nie wychodzi

Marcin:

10		n		n		10		35
	*		+		*		>
10+n		9+n		10+n		9+n		68

Ja mam tak.

jerey:

10n		35
	>
(9+n)(10+n)n		68

jerey: n w sumie wypadnie

jerey: A− zdarzenie sprzyjające ?

	10 1		n 1
A=		*		*2?

kyrtap: Marcin nie kminie twojego zapisu

Marcin: Bo ja prawdopodobieństwa nie kumam i robię to tak chaotycznie. Może dlatego Wynik się zgadza (robiłem metodą drzewka)

kyrtap: czekaj jeszcze pomyślę swoją metodą może się uda

Marcin: No kmiń kmiń. Tak się więcej nauczysz

kyrtap: chyba nic z tym zadaniem nie wymyślę

Marcin: Narysuj sobie drzewko. Ogólnie masz 10+n kul. Teraz dwa razy losujesz kule. Uwzględnij dwie możliwości, tzn najpierw czarna, później biała i odwrotnie. Po wyciągnięciu jednej kuli masz już n+9 kul

kyrtap: wiem ale myślałem że można to jakoś że wyliczę omegę i potem zdarzenie tak jak zawsze pewnie można jakoś ale nie wiem jak

Tyrmand: Jak zrobić zadanie 4.? Bo domyślam się że z podobieństwa, ale nie potrafię dojść do tego, dlaczego te trójkąty miałyby być podobne...

zombi: Jerey twoim sposobem

	n+1 2
Ω= =

	10 1		n 1
A= =		*

zombi: Patrz wyżej tam jest rozwiązanie razora i moje do zadania 4.

Marcin: Tyrmand popatrz gdzieś do góry. Tam masz rozwiązanie

kyrtap: mam Tyrmand rozpisać?

Karol: Czy podałeś dobrą odpowiedź do zadania 12

Tyrmand: czekaj, najpierw poszukam u góry

kyrtap:

	n+1 2
zombi czemu		?

zombi: n+10*

jerey:

	n+1 2
zombi ale dlaczego moc zbioru

mamy n kul czarnych i 10 białych a losujemy 2 bez zwracania :

10+n 2
	?

kyrtap: to ja tak robiłem zombi i dupa

jerey: ok, teraz mi sie wyswietliła czyli miałem ok , dzieki

Tyrmand: dobra, już kumam 4.

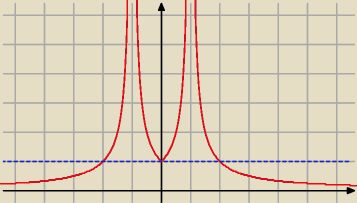
Marcin: Karol, a dlaczego według Ciebie zawodus podał złą?

zawodus: Widzę, że temat nadal żyje Dobra już wrzucam rozwiązanie "sławnego" zadania drugiego, którego nikt nie zrobił

zawodus: A tak w ogóle to jestem ciekaw czy interesuje was jeszcze jedna maturka, którą jeśli znajdę trochę czasu mógłbym ułożyć

kyrtap: ja jestem za zawodus

Tyrmand: 2. f(m)<0 dla a>0 f(m)>0 dla a<0

Tyrmand: ja też jestem za

zawodus: Tyrmand jesteś maturzystą? Może uzasadnisz skąd takie warunki i czy da nam to rozwiązanie zadania?

Karol: Widocznie jestem za głupi, byłbym wdzięczny gdyby ktoś powiedział mi co złego zrobiłem : Rozpocząłem od f(x)=1/x następnie przesunąłem o wektor 1 w prawo czyli f(x)= 1/x−1 , wszystko odbiłem z dołu do góry i f(x)= |1/x−1| po czym odbiłem wszystko z lewej do prawej |1/|x−1|| i wyszedł mi jakiś strasznie dziwny rysunek... Na tej stronie co Zawodus posłał, wychodzi inny wykres aniżeli ten co Ty posłałeś .

Saizou : a ja jestem przed a nie za

Marcin: No i ja też jestem za

zombi: Jasne zawodus, wrzucaj

zawodus: Wykres podany przez Marcina jest ok Karol nie ma czegoś takiego "odbiłem z lewej do prawej" Jeśli już to z prawej na lewą Po drugie

	1		1
|		| →(f(|x|)) → |		|
	x−1		|x|−1

zawodus: Miałem wrzucać zadanie nr 2, ale Tyrmand być może wie jak je rozwiązać, zatem poczekamy

Tyrmand: tak, jestem maturzystą −jeśli parabola ma ramiona skierowane w górę (czyli a>0), to oba miejsca zerowe muszą się znajdować po obu stronach argumentu "m", a zatem f(m) musi się znajdować pod osią dla a>0 −dla a<0 nad osią

kyrtap: ale wrzuć mi rozwiązanie prawdopodobieństwa bo widocznie take warunki które dałem czyli Ω = C² _n+10 A = C¹_n* C¹₁₀ nie są dobre

Tyrmand: prawdopodobieństwo, gdy coś się losuje kolejno, to chyba rzeczywiście najpewniej jest rozwiązać drzewkiem

kyrtap: ok w takim razie zrobię drzewkiem choć nie lubię tego sposobu

zawodus: Tyrmand dobrze tylko jeszcze wytłumacz wszystkim dlaczego nie piszesz warunku z deltą

Tyrmand: nie no, chyba trzeba jeszcze: m≠−1 żeby była funkcja kwadratowa Δ>0 tylko szczerze powiem że ta delta to taka trochę nierozwiązywalna

Marcin: Czyli nadal nic nie wiadomo

Tyrmand: z delty mi wyszło coś takiego: −24m³+24m²−32m+228>0

Marcin: Tak jak każdemu.

Tyrmand: czyli wg wolframa w wersji przybliżonej: m<2,2642

Saizou : może chodzi o to że skoro a*f(m)<0 dla to z warunku x₁<m<x₂ muszą istnieć pierwiastki w sumie już to czuję ale nie wiem jak to zapisać xd

zawodus: Dobrze, to w takim razie ja podam rozwiązanie, bo niestety, ale nikt nie potrafi uzasadnić prostego faktu Rozwiązanie zadania 2 Wyznacz wszystkie wartości parametru m, dla których pierwiastki rzeczywiste równania (m+1)x²+14x+6m²+8 spełniają warunek x₁<m<x₂ Zadanie specjalnie tak dobrane, żeby delty nie dało się prosto policzyć. Interesuje nas, aby liczba m znajdowała się pomiędzy x₁ oraz x₂. Wystarczające są do tego warunki: 1. a>0 i f(m)<0 2. a<0 i f(m)>0 Można je połączyć w jeden warunek a*f(m)<0 U nas powstaje nierówność do rozwiązania (m+1)(m³+7m²+14m+8)<0 Ta nierówność się już elegancko liczy Odpowiedź taka jak podana wyżej m∊(−4,−2) W tym zadaniu nie jest w cale potrzebny warunek Δ>0 (dlaczego?)

Bogdan: Dzień dobry. zawodus, czy zadanie 9 czeka na rozwiązanie?

zawodus: Cześć Bogdan Część osób twierdzi, że zrobiła, ale jeśli masz ochotę to nie odmówię ci tej przyjemności

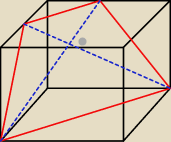
Marcin: Witaj Bogdanie. Ja sobie jakoś z tym poradziłem, ale może ktoś zapisałby taki w pełni dokładny dowód, na pełną ilość punktów

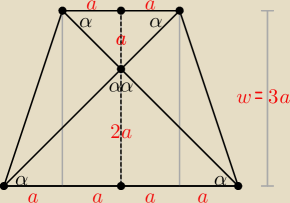
Bogdan: Myślę, że mój rysunek zamieszczony tu 248694 i ten rysunek wyjaśniają sprawę. α = 45^o

Karol: Witam, mam pytanie odnośnie zadania 11. Narysowałem sobie drzewko i wyszła mi nierówność :

10		n		10		n		35
	*		+		*		>
10+n		9+n		10+n		9+n		68

Z tego 35n² − 695n + 3150 < 0 √Δ = 205 n1 = 7 n2 ~12,8 Zrobiłem gdzieś błąd?

zawodus: Zła nierówność, bo napisałeś dwa razy to samo po znaku "+"

Tyrmand: przecież dobrze wyszło

Marcin: Karol według mnie, to teraz liczysz dwa razy to samo.

ciekawy: Mi wyszlo tak samo jak Karolowi sposobem jereya

Cash18: Karol wynik okej, tylko znak się coś nie zgadza. Pamiętaj że wynik to wszystkie kule − czyli trzeba też dodać 10 białych

Tyrmand: dokładnie, +10

Cash18: A mógłbym ktoś mi rozpisać zadanie z wielomianem, bo nie mam pomysłu − Ktoś widzę już prosił, ale nie spotkało się to z żadnym odzewem

Marcin: Jedynym możliwym pierwiastkiem, który jest liczbą pierwszą jest dwójka Próbuj dalej

Cash18: No właśnie do tego doszedłem sam, ale dalej nic nie mogę wyliczyć z tego równania

Tyrmand: A Ty to Marcin jakoś zauważyłeś? Bo mi to z 4 linijki zajęło że tą liczbą pierwszą jest tylko dwójka

Cash18: To łatwo było zauważyć z twierdzenie o p. wymiernych

Marcin: Twierdzenie o pierwiastkach wymiernych. Skoro wszystkie możliwe pierwiastki całkowite, to 1, −1, 2, −2, to widać, że tylko 2 jest liczbą pierwszą

Cash18: To wiem ale jak mam W(2)=0 to tutaj się komplikuje, niby nic wielkiego ale nic nie wychodzi z układu.

Marcin: Napisz co Ci wychodzi, jeżeli podstawiasz 2 i przyrównujesz wielomian do 0.

Tyrmand: O, to jednak twierdzenia się przydają

Bet: Podesłałby mi ktoś rozwiązania arkuszy z tegorocznych maturek R z zadania.info?

Marcin: Wszystkich?

Bet: Mhmm z tego roku 2−8 zestaw z rozszerzenia 2014

Bet: Opornie mi to idzie, im więcej robię tym mniej wiem

cash18: po wielu trudach, wynik wyszedl

Marcin: Łap zestaw 2: http://www.webpagescreenshot.info/i3/5363cbf5ef8749-74622433

Bet: małe to trochę

Marcin: Powiększ sobie Przeglądarka Ci to specjalnie zmniejszyła

zadaj: Dobrze mam na razie 5 zadanie W(2)=ab−4b−2a−1

Bet: Wymiary : 43px × 300px więc nie przeglądarka, tylko to jakaś miniaturka chyba :<

zadaj: Przez chrome odpal.

Bet: dziękuje ślicznie cholerny firefox

Marcin:

zawodus: Zadaj teraz to przyrównaj do zera i wyznacz liczby a i b spełniające dane równanie

zadaj: ab−4b−2a−1=0 ab−4b=2a+1 b(a−4)=2a+1

	2a+1
b=
	a−4

Saizou : ab−4b−2a−1=0 b(a−4)−2a+8−8−1=0 b(a−4)−2(a−4)=9 (a−4)(b−2)=9 a skoro to liczby naturalne to 9=9*1 lub 9=3*3

Marcin:

	2(a−4) +9		9
b=		→ 2+		Widać teraz, że żeby to były liczby całkowite dodatnie, to za
	a−4		a−4

a możesz wstawić 5, 7 lub 13

zadaj: dzięki.

zawodus: Zapraszam na maturkę w wersji mini

Matejko: zaraz zrobie