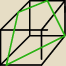
Sześcian przecięto Matejko: Sześcian przecięto płaszczyzną przechodzącą przez przekątną dolnej podstawy i środki dwóch krawędzi górnej podstawy. Pole otrzymanego przekroju jest równe 40,5cm². Oblicz jego objętość. nie wyszedł mi ten sześcian ale wiecie o co chodzi zielonym oznaczyłem ten przekrój czyli trapez równoramienny MOJE OBLICZENIA I WNIOSKI: dolna przekątna trapezu to a√2 a górna to ^a√2₂ z twierdzenia pitagorasa licze ramie: c−ramie trapezu a²+^a₂²=c² czyli c=^√5a₂ i teraz wysokość tego trapezu z pitagorasa: aha i dolną postawe podzieliłem na ^a√2₂ i 2 razy ^a√2₄

	3√2
wyszła mi
	4

i dalej ze zworu na pole i podstawiałem i wyszło mi a=12 a ma być a=6. Co mam źle? Prosze o pomoc

Matejko: mam xD błąd obliczeniowy a tyle się opisałem

Janek191:

	5
c2 = a2 + (12 a)2 =		a2
	4

p₁ = a√2 p₂ = 0,5 a√2 x = ( p₁ − p₂): 2 = 0,25 a√2 = ¹₄ a√2 ⇒ x² = ¹₈a² zatem c² = x² + h²

	5		1		9
h2 =		a2 −		a2 =		a2
	4		8		8

	3		3√2
h =		a =		a
	2√2		4

Pole trapezu

	3√2
P = 0,5*( p1 + p2)*h = 0,5*1,5 a√2*		a = 40,5 / * 4
	4

4,5 a² = 162 / : 4,5 a² = 36 a = 6 V = 6³ = 216 ===========

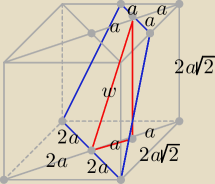Bogdan: Odpowiednio oznaczając potrzebne do rozwiązania długości możemy uniknąć wielu rachunków, wtedy prościej i w krótszym czasie uzyskamy rozwiązanie.

	1		81		9		3
w = √8a2 + a2 = 3a,		*3a*6a =		⇒ a2 =		⇒ a =
	2		2		2		√2

	3
V = (2a√2)3 = (2*		*√2)3 = 63 = 216
	√2

Bogdan: Nie trzeba trzymać się kurczowo wyuczonych oznaczeń, np. nie musimy oznaczać krawędzi sześcianu literką a. Warto przyjąć przyjazne oznaczenia. W tym zadaniu oznaczyłem długość przekątnej kwadratu 4a

kasiaxm: Matejko: ''dolna przekątna trapezu to a√2 a górna to a√2/2'' Jak obliczyłeś to a√2/2?