Pilnie potrzebuje :) kamciol28: Oblicz równanie symetralnej odcinka AB gdzie A(1;4)) B(−3;−4) Wytłumaczcie mi to krok po kroku bo jakoś załapać tego nie moge

5-latek: Najpierw napisz definicje symetralnej Wiec co to jest symetralna ?

kamciol28: Prosta przechodząca przez ten odcinek przez środek i pod kątem prostym

kamciol28: Czyli do wzoru na środek odcinka wyjdzie mi że środek jest w punkcie S=(2,4)

pigor: ..., to twoje S=(2,4) nie jest środkiem odcinka AB .

5-latek: Teraz wylicz wspolczynnik kierunkowy prostej AB (nie musisz pisac calego rownania i rownaie prostej prostopadlej do AB i przechodzacej przez punkt S Wiadomo jaki jest warunek na to aby proste byly prostopadle

kamciol28: Pigor więc wytłumacz dlaczego

pigor: .. tu środek AB : S=(¹₂(1−3)),¹₂(4−4))= (−1,0) i tyle .

kamciol28: faktycznie znaki miałem inaczej na wzorze napisane i zamiast odejjmować to dodałem, dzieki a współczynnik kierunkowy to bedzie − 2/4 czy też coś mi sie pomyliło?

5-latek:

	y2−y1
tgα=a=		= policz
	x2−x1

kamciol28: no to właśnie liczyłem i chce sie dowiedziec czy znowu cos źle musze to ogarnąc jakoś do jutra

5-latek:

	−4−4		−8
a=		=		= ile ?
	−3−1		−4

pigor: ,,, a wektor kierunkowy prostej AB to : u= [−3−1,−4−4]= [−4,−8]= [−4[1,2]= [1,2] i jest to zarazem wektor normalny [A,B] szukanej symetralnej s w postaci ogólnej, czyli s: 1x+2y+C=0 i S=(−1,0)∊s, więc −1+2*0+C=0 ⇒ C=−1, zatem x+2y−1=0 − szukane równanie symetralnej odcinka AB. ...

kamciol28: 2? kur... to czemu ja mam wszystkie wzory anpisane na odwrót.. ja miałem y1−y2 / x1 −x2

kamciol28: nie.. to jest dla mnie nie do ogarnięcia.. ; /

kamciol28: pigor jesteś jeszcze? Bo z tym zadanie dałem sobie spokój już, a możesz mi inne wytłumaczyć

5-latek: Pieprzysz glupoty . Popraw wzory i licz dalej pigor Ci pokazal jak to zrobic na wektorach i rownaaie w postaci ogolnej Jesli tego nie ogarniasz to rob tak jak robiliscie na lekcji czyli a= Ile ?

kamciol28: no a= 2

5-latek: Jaki jest warunek na to aby dwie proste byly prostopadle ?

5-latek: https://matematykaszkolna.pl/strona/42.html patrz tutaj

kamciol28: i co mi to mówi że a1 *a2 = −1 . jedno a mam wyliczone i wynosi 2

kamciol28: i co mi to mówi że a1 *a2 = −1 . jedno a mam wyliczone i wynosi 2

5-latek: to napisz teraz jaki wspolczynnik kierunkowy bedzie miala prosta prostopadla do prostej AB jesli wspolczynnik kierunkowy prostej AB a=2

kamciol28: i co mi to mówi że a1 *a2 = −1 . jedno a mam wyliczone i wynosi 2

5-latek:

	−1
no np to ze jesli a1=2 to 2*a2=−1 to a2=		to a2 =ile ? gdzie a2 to
	2

wspolczynnik kierunkowy prostej prostopadlej do AB

kamciol28: −1/2 ?

kamciol28: a1= 2 a2= −1/2

PW: kamcio, jeżeli tak jest za trudno, to zrób tak jak cyrklem − punkty na symetralnej są jednakowo odległe od A i od B, czyli (piszę kwadraty odległości) współrzędne każdego punktu (x,y) na symetralnej spełniają równanie (x − 1)² + (y − 4)² = (x + 3)² + (y + 4)². Popatrz − nawet nie rozwiązując można zauważyć, że zredukują się x² oraz y² i zostanie piękne równanie liniowe dwóch zmiennych, czyli równanie prostej.

5-latek: Pozniej sobie przeanalizyjesz sposob ktory napisal PW Pozdrawiam TO teraz rownanie prostej ktorej szukamy to bedzie mialo postac

	1
y=a2x+b to y=−		x+b . Wstaw wspolrzedne punktu S do tego rownania i wylicz z tego b i
	2

napisz rownanie tej prostej

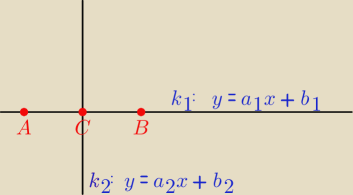
Bogdan: Krok po kroku.

	1 − 3		4 − 4
A = (1, 4), B = (−3, −4), środek AB to C = (		,		) = (−1, 0)
	2		2

	−4 − 4
Prosta przechodząca przez A i B to prosta k1: y = a1x + b1, a1 =		= 2
	−3 − 1

Prosta przechodząca przez C(−1, 0) i prostopadła do prostej k₁ to prosta k₂: y = a₂x + b₂

	1
k1 ⊥ k2 ⇒ a1 * a2 = −1 ⇒ 2 * a2 = −1 ⇒ a2 = −
	2

	1		1		1
k2: y = −		(x + 1) + 0 ⇒ y = −		x −
	2		2		2

5-latek: Witam No to teraz ma jak dloni wszystko . Nie powienien juz miec z tym problemu

Bogdan: Dobry wieczór

5-latek: Moze jeszce sie nie zniechecil masz kolega

kamciol28: No jakoś sobie analizuje to wszystko i do wszystkiego powoli dochodze także dzieki koledzy jak coś to jeszcze bede pisał

kamciol28: Jesteście jeszcze panowie?