Planimetria bezendu: Ramiona kąta ostrego o mierze 2x przecięto prostą k prostopadłą do dwusiecznej kąta, która jest odległa o d od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej k . Oblicz odległość środków tych okręgów Wstawiam nowy team bo tamten zamienił się w wątek o lekturach...

kyrtap: Może i ten się zmieni?

bezendu: ?

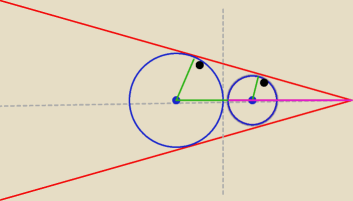
Marcin: różowa linia=d To chyba będzie coś takiego, ale dalej baw się sam, bo idę czytać

kyrtap: jak mnie wzrok nie myli już coś podobnego było na maturze z operonu w tym roku

kyrtap: bezendu zrobiłeś czy pomóc?

bezendu: Zrobiłem.

kyrtap: to git

kyrtap: chyba nie było trudne?

bezendu: Trudne

Marcin: Widzę że Ci kyrtap wyszło Zapisz swoje obliczenia, to później sobie zobaczę

Maslanek: Oznaczając r, R − promienie odpowiednich okręgów Z twierdzenia Talesa:

d−r		d+R
	=
r		R

dR−rR=dr+rR dR−dr−2rR=0 R(d−2r)=dr

	dr
R=
	d−2r

	dr		dr−2r2+dr		2dr−2r2
I r+R=r+		=		=
	d−2r		d−2r		dr

	r
Dodatkowo: sinx=
	d−r

Tak to powinno lecieć? Bo ja to już dętka

kyrtap: ja podobnie zrobiłem Maślanek powołałem się na podobieństwo trójkątów ale to to samo praktycznie

kyrtap: Bezendu podziwiam Cię wiesz że masz taki zapał?

bezendu: Tzn?

kyrtap: no do matmy

bezendu: brak talentu=ciężka praca i tyle

kyrtap: no ja też nie mam talentu

Maslanek: Ale marudzicie Robienie zadań wyrabia intuicję

bezendu: Dlatego napisałem, że ciężka praca

kyrtap: Chcesz podobne zadanko?

bezendu: Nom

kyrtap:

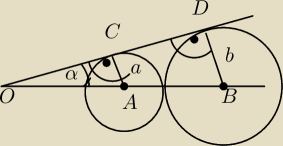
	2√ab
Uwzględniają dane przedstawione na rysunku wykaż że cosα=
	a+b

kyrtap: Uwzględniając *

Mila: Do rys. Marcina

	r
1) sinx=		⇔
	d−r

	dsinx
r=
	1+sinx

	R
2) sinx=		⇔
	d+R

	d*sinx
R=
	1−sinx

	dsinx		d*sinx
r+R=		+		⇔
	1+sinx		1−sinx

	1−sinx+1+sinx		2dsinx
r+R= dsinx*(		=
	(1−sinx)*(1+sinx)		cos2x

kyrtap: Mila nie rozwiązuj narazie drugiego

bezendu: Z telasa:

OA		OC+CD
	=
a		b

a(|OC|+|CD|)=b|OC| a|OC|+a|CD|=b|OC| a|OC|−b|OC|=−a|CD| |OC|(a−b)=−a|CD|

	−a|CD|
|OC|=
	a−b)

Hmm ?

Marcin: Maslanek, ale przecież nie miałeś w zadaniu od bezendu danego promienia

kyrtap: czemu piszesz OC + CD zamiast OA + AB?

bezendu: właśnie coś popsułem...

Maslanek: Dlatego wprowadziłem ten sinus na końcu. Niech dobre dusze sobie doliczą

Marcin: Ok, rozumiem

Eta:

	b−a
sinα=
	b+a

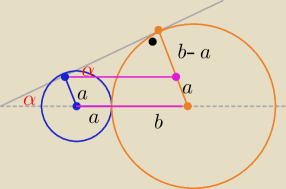
cosα= + √1−sin²α=........... = ... teza

Wazyl: |OC|=x |CD|=y y²=√(a+b)²−(a−b)² ⇒ y=2√ab

x		x+2√ab
	=
a		b

(x+2√ab)*a=bx xa−bx+2a√ab=0

	2a√ab
x=−
	a−b

	4a3b
|OA|2=a2+
	(a−b)2

	a4−2a3b+a2b2+4a3b
|OA|2=
	(a−b)2

	a2(a+b)2		a(a+b)
|OA|2=		⇒ |OA|=
	(a−b)2		a−b

	|OC|
cosα=
	|OA|

	2a√ab   a−b		2√ab
cosα=		⇒ cosα=
	a(a+b)   a−b		a+b

kyrtap:

bezendu: Wazyl sam chciałem pomęczyć, nie musiałeś wstawiać rozwiązania od A do Z... Eta a moim sposobem ?

Wazyl: Jeden mały fsitaszek:

	bla bla
a<b ⇒ |OA|=
	b−a

Wazyl: Przepraszam bezendu

bezendu: Nie mówię, że nie masz robić ale jak zadanie było do mnie ja próbuje robić a tu ktoś mi gotowca sypie...

Eta:

kyrtap: Bezendu mogę Ci dać jeszcze jedno? jak chcesz?

bezendu: Eta skąd taki pomysł ?

bezendu: Na razie to chcę dokończyć

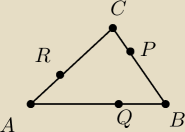
Wazyl: Mam przeprosinowe zadanie dla Ciebie: Pole trójkąta ABC jest równe 28. Oblicz pole trójkąta którego boki zawarte są wprostych AP, BQ i CR, jeśli |RB=¹₃|AB|, |PC|=¹₃|BC| |QA|=¹₃|CA|

kyrtap: Wazyl

bezendu: Wazyl lepiej tamto mi wytłumacz bo robiłeś podobnie jak ja

Wazyl: A to bardzo prosto. |OC| dobrze wyznaczyłeś. Potrzebne Ci jeszcze tylko |OA| a to z pitagorasa łatwo.

	|OC|
cosα=		i po sprawie.
	|OA|

Obliczenia nie wyglądają przyjemnie ale sama metodologia jest bardzo prosta: tales potem pitagoras A jak z moim trójkątem?

bezendu: A no dobra ja właśnie też myślałem o pitagorasie ciężko z Twoim trójkątem

Wazyl: Zostawiam Ci trójkąt na noc. Ja już lece spać. Dobranoc wszystkim. bezendu jutro czekam na odpowiedź.

bezendu: Dobranoc

zawodus: Wazyl to twoje zadanie coś nie tak

Wazyl: Dlaczego zawodus ?

Wazyl: tak wkradł się mały błąd CQ i BR

zawodus: Ciekawe czy sam umiesz je rozwiązać To bardziej zadanie olimpijskie

bezendu: A czy w tych zadaniach z okręgami trzeba korzystać z Talesa anie można z trójkątów podobnych ?

Mila: Korzystaj z tego, z czego można . Wygodniej z Δpodobnych to korzystaj.

bezendu: Tak się pytam, chciałem też zrobić z trójkątów a nie z Tw Talesa.

zawodus: Ja jestem zdania że na maturze to każdy sposób prowadzący do celu jest ok to nie czas na szukanie najprostszego rozwiązania

Kamix: Nie wiem czemu ale rozumiem Bezendu, też mam ogromne problemy z planimetrią, ale odpuściłem ją całkowicie, bo uważam, że albo mi się uda i coś wykombinuję, albo nie, teraz na naukę już za późno. Też bym wolał korzystać z Δ podobnych, nie wiem czemu, ale układanie tych stosunków boków do Talesa w takich bardziej rozrysowanych przykładach sprawia mi problem...

bezendu: Ja coś tam już rozumiem, ale na maturze liczę na łut szczęścia czyli twierdzenie cosinusów i sinusów.

Mila: Poradzicie sobie, ale rozwiązujcie zadania, niekonicznie trudne, ale takie by utrwalać wiadomości i coraz więcej widziec.

bezendu: Ja do 04:00 wczoraj robiłem, już nie wiem jakie mam tę zadania robić ? Tę z arkuszy już nie sprawiają mi problemów.

Mila: Stanowczo za dużo pracujesz, mózg wysiada, nerwy Cię zjadają, przecież widzę, że wpadasz w furię z byle jakiego powodu. Myśmy mówili, że mózg się lasuje, cokolwiek to znaczy i wtedy był obowiązkowo odpoczynek.

bezendu: Chcę napisać na 90%+ Matematykę R

bezendu: Ma ktoś podobne zadanie to tego co wstawiłem ?

Piotr 10: A robiles maturke z sierpnia 2013 poziom R ?

Piotr 10: Tam jest jedno podobne zadanko z okregami

bezendu: robiłem

bezendu: Podbijam proszę o kilka zadań tego typu na wieczór

Mila: To rozwiązywałeś? https://matematykaszkolna.pl/forum/248420.html

Mila: 1) Promień okregu ma dł. 25 cm,zaś dwie równoległe cięciwy maja długości 14 cm i 40 cm. Oblicz odległość między tymi cięciwami.

bezendu: Tak, rozwiązałem. Ale chodzi mi bardziej o takie na literkach zadania. ?

Mila: 2) Pole trapezu równoramiennego opisanego na okręgu wynosi S. Oblicz długość ramienia trapezu, wiedząc, że kąt ostry trapezu jest równy 30^o.

bezendu:

a+b
	*h=S /2
2

(a+b)h=2s

	2s
h=
	(a+b)

	b−a
tg30=U{h}{
	2

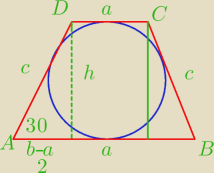
	√3((b−a)
h=
	6

Nie wiem czy ok ?

Mila: Dobrze, Pierwsze 3 liniki (+).Dalej chyba nie przyda się. Nie wykorzystałeś informacji, że w trapez można wpisać okrąg.

bezendu: a+b=2c o to chodzi ?

Mila: Tak.

bezendu:

a+b
	*h=S
2

ch=s

	s
h=
	c

	h
sin30=
	c

2S=c²

	c2
s=
	2

	c
h=
	2

	a+b		c
P=		*
	2		2

	c
P=c*
	2

	c2
P=
	2

coś nie tak ?

Mila: Masz pbliczyć długość ramienia: otrzymałeś w 5 linijce: 2S=c²⇔ c=√2S i to już koniec.

bezendu: Ja nie doczytałem, tutaj takie dobre dusze pomogą zawsze

Eta:

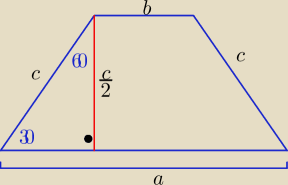
	a+b		c
a+b=2c ⇒		=c , h=
	2		2

	c
S=c*		⇒ c= √2S
	2

bezendu: Kolejna dobra duszyczka

Eta: Która?

bezendu: Mila , Eta szkoda, że to już prawie koniec przygody z maturą

Eta: ........ zawsze możesz sobie przedłużyć o...... np. rok

bezendu: Jak już szkołę skończyłem

Eta: Chodzi mi o przedłużenie ........"przygody z maturą" ?

bezendu: Jak napisze na 30% to powtórzę

Eta: ... ma być 100% !

bezendu: W myślach tyle jest Będziesz jeszcze na forum ?

Wazyl: Bezendu ja czekam na moje zadanie ciągle!

bezendu: To zadanie olimpijskie Wazy wiedziałem, że mnie dopadniesz z tym