:( matma: BARDZO PROSZE O POMOC dWA OKRĘGI o promieniach r oraz R są styczne zewnętrznie. Oblicz odległość ich punktu styczności od wspólnej stycznej zewnętrznej.

matma: ?

PW: Po narysowaniu dwóch okręgów i stycznej narysuj obrazy tych okręgów w symetrii względem tej stycznej. Zobaczysz trapez, którego jedną z podstaw jest 2R, a drugą 2r, zaś ramiona mają długości R+r. Podstawy są prostopadłe do stycznej, odcinek łączący wspólne punkty okręgów − też. Mamy zatem trapez równoramienny, na którego ramionach odcinek równoległy do podstaw wyznaczył

	r
punkty dzielące ramiona w stosunku		. Długość tego odcinka − równa podwojonej szukanej
	R

odległości − powinna się dać obliczyć (ramiona kąta przecięte trzema równoległymi).

PW: https://matematykaszkolna.pl/forum/248440.html − Irena1 już zrealizowała rano, moje rady nie są potrzebne.

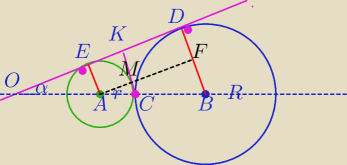
Mila: Realizuję pomysł PW. M− punkt przecięcia CK i AF CK=r+x, x=CM ΔAMC∼ΔABF

r		r+R
	=		⇔
x		FB

r		r+R
	=		⇔
x		R−r

	r*(R−r)
x=
	R+r

|CK|=x+r

	r*R−r2
|CK|=		+r
	R+r

	r*R−r2+r*(R+r)
|CK|=
	R+r

	2r*R
|CK|=
	R+r

PW: Milu, wykonałaś te straszne rachunki z pięknym skutkiem. Szkoda tylko, że matma zadał(a) pytanie w dwóch miejscach i w ogóle się nie interesuje.

Mila: Właśnie wg Twojego pomysłu rachunki proste Może komuś przyda się.

pi: ja wykorzystam

Mila: