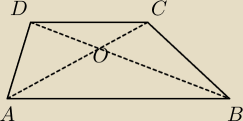
planimetria w trapezie jhonie: wykaż, że PΔ DOC * PΔ ABO = PΔ ADO² opcjonalnie korzystając z podobieństwa trójkątów

pigor: .... , widzę to tak :

PΔAOB		12AO*hAO		AO
	=		=		,
PΔCOB		12OC*hOC		OC

analogicznie

PΔAOD		12AO*h'AO		AO
	=		=		,
PΔCOD		12OC*h'OC		OC

	PΔAOB		PΔAOD
stąd(*)		=
	PΔCOB		PΔCOD

ale P_ΔAOD = P_ΔCOB (dowód równości tych pól prosty i nieraz był na forum), to z (*) i własności proporcji :

	PΔAOB		PΔAOD
		=		⇔
	PΔAOD		PΔCOD

⇔ P_ΔCOD * P_ΔAOB= P²_ΔAOD c.n.w. . ...

jhonie: nie do końca rozumiem dlaczego ¹₂ AO*hAO mógłbyś to jakoś wytłymaczyć?

jhonie: już nieważne, bardzo dziękuję za pomoc

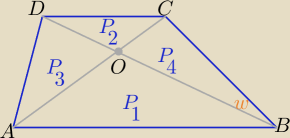
Eta: Trójkąty ABO i DCO są podobne z cechy skali k>0

	P1
to:		= k2 ⇒P1=k2*P2
	P2

i P₃=k*P₂ to P₃²=k²*P₂² =k²*P₂*P₂ ⇒ P₃²= P₁*P₂ c.n.u

Eta: https://matematykaszkolna.pl/forum/191513.html