arkusz kyrtap: ARKUSZ 2

	a		a
1.Liczby dodatnie a,b,c spełniają warunki:		=2 i		=3.Uporządkuj liczby a,b,c od
	b+c		b−c

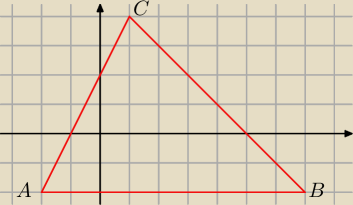
najmniejszej do największej. 2. Na rysunku przedstawiono trójkąt ABC: a) Odczytaj z rysunku współrzędne wierzchołków trójkąta ABC. b) Napisz równania prostych AC i BC. c) Opisz za pomocą układu nierówności liniowych zbiór wszystkich punktów (x,y) należących do trójkąta ABC. 3. Ciąg(an) określony wzorem rekurencyjnym a1=m a2=2m (klamra) a_n+1=2a_n−a_n−1 gdzie m jest liczbą naturalną.Wykaż,że każda liczba naturalna podzielona przez m jest wyrazem tego ciągu. 4.Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu (x−16)² + y² = 4 jest okrąg o równaniu (x − 8)² + (y − 4)² = 36 a skala tej jednokładności jest liczbą ujemną. 5. Wierzchołki trójkąta równobocznego ABC są punktami paraboli y = −x² + 6x . Punkt C jest jej wierzchołkiem, a bok AB jest równoległy do osi Ox . Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.

	3
6. Oblicz wartość sin3x +cos3x jeśli wiadomo że sinx + cosx =		.
	4

7. Narysuj wykres funkcji f(m) która jest liczbą rozwiązań układu równań z parametrem m. (m−1)x+3y=5 (klamra) mx − 2y = 4

	mx		m+1
8. Dla jakich wartości parametru m równanie		+		= x+1 ma dwa pierwiastki x1
	m−1		x

	1		1
i x2 spełniające warunek		+		<2m+1?
	x1		x2

9. Z pojemnika w którym jest n kul białych, 2n kul zielonych i 3n kul czerwonych losujemy jednocześnie trzy kule. Prawdopodobieństwo otrzymania w tym doświadczeniu kuli białej , zielonej i czerwonej jest równe 0,3. Oblicz ile kul jest w pojemniku. 10.Walec i stożek mają tworzące równej długości, równe pola powierzchni bocznych i równe objętości. Oblicz cosinus kąta nachylenia tworzącej stożka do płaszczyzny podstawy.

kyrtap: ta jeszcze chyba jest prostsza

Saizou : dzisiaj już nie liczę, znaczy się tej nocy, nie chce mi się

Saizou : jeszcze przerysuje ten trójkąt z zad. 2

Saizou : *przerysuj

kyrtap: a sorki dzięki saizou że zwróciłeś uwagę

zombi: 1. c<b<a?

kyrtap: pretty good

kyrtap: nie wiem jak wam narysować trójkąt

Marcin: a=7c b=5c a>b>c. Jakoś tak.

Saizou : w układzie współrzędnych

Marcin: Wyślij mi zdjęcie to przerysuję

kyrtap: dobra

kyrtap: Panie Marcinie masz?

Marcin: Ciąg z 3: m, 2m, 3m, 4m, 5m, 6m, 7m, 8m, 9m.. Tak mi się przynajmniej wydaje

Marcin: a mam, chwilka

Marcin:

Marcin: To zadanie jest przecież banalne. Mamy odczytywać współrzędne punktów A B i C?

kyrtap: a ile to roboty?

Marcin: No właśnie to żadna robota Patryku

kyrtap: Good job

kyrtap: Taka mówisz będzie matura w tym roku?

Marcin: Coś w ten deseń

kyrtap: Ja jutro się za biorę za te zadania z którymi mam problemy

kyrtap: bo już dzisiaj padam

Marcin: Przecież jeszcze jest bardzo wcześnie

kyrtap: ale byłem z kumplem na kebsie a jak się zje na wieczór to mi się spać chce

Marcin: Chętnie sam zjadłbym kebsa

kyrtap: I jak Marcin robisz te banalne zadanka?

Marcin: Ja nie powiedziałem że wszystkie są banalne Jednokładności nawet nie ruszam

kyrtap: Ruszaj ruszaj bo pewnie proste

Marcin: Ja nigdy nie miałem w szkole ani prawdopodobieństwa, ani wektorów, ani jednokładności. Praktycznie niczego nie miałem. Dlatego mam teraz takie braki w niektórych działach. Chociaż staram się jak mogę

bezendu: Gdzie jest to zadanie z jednokładnością ? Mogę się pokusić o nie mniam

bezendu: .Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu (x−16)2 + y2 = 4 jest okrąg o równaniu (x − 8)2 + (y − 4)2 = 36 a skala tej jednokładności jest liczbą ujemną. o to chodzi Panowie ?

Marcin: Tak. Ja nie mówię że to jest trudne, ale nigdy tego nie robiłem

kyrtap: Marcin ile ty byś wiedział których nie robiłem

kyrtap: rzeczy*

Marcin: Wolę nie wiedzieć

bezendu: O₁: (x−16)²+y²=4 S₁(16,0) r=2 O₂:(x−8)²+(y−4)²=36 S₂=(6,4) r=6 k=3 [6−a, 4−b]=3[16−a, 0−b] 6−a=48−3a 2a=54 a=27 4−b=−3b 2b=−4 b=−2

Marcin: Nie wydaje się trudne Zastanawiam się czy ogarnąć to przed maturą, skoro od kiedy jest nowa matura, to jednokładności na niej nie było

kyrtap: jednokładność to wektory więc nic trudnego

bezendu: takie zadanie sobie życzę na maturce maj 2014 !

Marcin: Chętnie bym Ci tego pożyczył, ale ja nie chcę jednokładności

Marcin: Może to głupie pytanie, ale dlaczego [6−a, 4−b]=3[16−a, 0−b], a nie 3[6−a, 4−b]=[16−a, 0−b]?

bezendu: Zobacz co jest obrazem czego

Marcin: Czyli zawsze jest k[np okrąg]=[obraz tego okegu]?

kyrtap: Bezendu specjalnie dałem to zadanie wiesz dlaczego?

kyrtap: nie w sumie nie jakoś źle tam policzyłeś

kyrtap: bezendu zamiast 6 powinno być 8

bezendu: ja zryapłem bo źle popatrzyłem...

bezendu: no czemu dałeś ?

bezendu: Panowie 40 brył jeszcze, uciekam do pracy

Marcin: Dzięki za odpowiedź

kyrtap: ja mam newsa : Podobno będzie powtarzany egzamin gimnazjalny w całej Polsce

Marcin: ściemniasz

kyrtap: a nie sory w niektórych szkołach

Marcin: No ja Ci gwarantuję, że z maturą będzie podobnie

bezendu: 1.Pomaluj drwala 2. Wpisz pesel

kyrtap: Bezendu jak tam w maju piszesz na 100 pro maturę ?

bezendu: Chyba bez tego zera z tyłu

Marcin: Z takimi tekstami to się z kyrtapem dogadacie

kyrtap: jakie teksty?

Marcin: Że słabo pójdzie matura

kyrtap: aaaa no bo ja czasami tak pierdziele nie od rzeczy

bezendu: W sumie miałem mieć tylko 30% wiec napiszę na 303%

Marcin: Ja jeszcze kilka miesięcy temu w ogóle nie myślałem o rozszerzeniu Na pierwszej deklaracji maturalnej go z resztą nie miałem

kyrtap: a co Marcin Cię skusiło ?

Marcin: Stwierdziłem, że nie chce mi się iść do pracy

kyrtap: Cztery liczby dodatnie a,b,c,d w podanej kolejności, tworzą ciąg geometryczny.Zatem liczby logd,logc,logb ,log a (w podanej kolejności) tworzą A) ciąg geometryczny o ilorazie log d

	c
B) ciąg arytmetyczny o różnicy log
	d

C) ciąg arytmetyczny o różnicy log d

	d
D) ciąg arytmetyczny o różnicy log
	c

Marcin: https://matematykaszkolna.pl/forum/247996.html Poryte. To jest z podstawy i kojarzę to zadnie.

kyrtap: Tak przeglądając arkusz zauważyłem że dość trudne

Marcin: Ja bym jakoś tak kombinował a=a b=aq c=aq² d=aq³ Teraz mamy ciąg logag³, logaq², logaq, loga Czyli widać, że to będzie a₁=logaq³ r= dzielenie przez logq

Marcin: Nawet nie tyle dzielenie, co odejmowanie logq

kyrtap: dobra jak wszystkim dobrej nocy

Marcin: No dobranoc

zawodus: Wystarczy przyjąć a=10 b=100 c=1000 d=10000 Logarytmy to 4.3.2.1 Teraz widać co tonza ciąg

zawodus: Wystarczy przyjąć a=10 b=100 c=1000 d=10000 Logarytmy to 4.3.2.1 Teraz widać co tonza ciąg

bezendu: Nikt nie robi więc zrobię z nudy:

	3
6. Oblicz wartość sin3x +cos3x jeśli wiadomo że sinx+cosx=
	4

sin³x+cos³x=(sinx+cosx)(sin²x−sinxcosx+cos²x) =(sinx+cosx)(1−sinxcosx)

	3
sinx+cosx=		/2
	4

	9
sin2x+2sinxcosx+cos2x=
	16

	9
2sinxcosx=		−1
	16

	7
sinxcosx=
	18

	4		7		22
sin3x+cos3x=		*(1−		)=
	3		18		27

bezendu: zadanie 9 1 kula biała 2 kule zielone 3 kule czerwone

kyrtap: Bezendu dla innych może za trudne

bezendu: Nie wnikam, bo ja przejmuje się swoją planimetrią.

pigor: ..., zad.9. Z pojemnika w którym jest n kul białych, 2n kul zielonych i 3n kul czerwonych losujemy jednocześnie trzy kule. Prawdopodobieństwo otrzymania w tym doświadczeniu kuli białej , zielonej i czerwonej jest równe 0,3. Oblicz, ile kul jest w pojemniku. −−−−−−−−−−−−−−−−−−−−−−−−−−− ..., ?=n∊N₊

n*2n*3n		6n3		3
	= 0,3 ⇔		=		⇔
6n 3		n(6n−1)(6n−2)		10

	2n2		1
⇔		=		⇔ ... ⇔ n=1 ⇒
	(6n−1)(6n−2)		10

odp. 6n= 6*1= 6 − szukana liczba kul w pojemniku . ...