ciagi jakubs: Trzy liczby tworzą ciąg geometryczny. Jeżeli do drugiej liczby dodamy 9, to ciąg ten zmieni się w arytmetyczny. Jeżeli zaś od drugiej liczby nowego ciągu arytmetycznego odejmiemy 1, to tak otrzymany ciąg będzie znów geometryczny. Znajdź te liczby a,b,c − c. geom. a,b+9,c − c. arytm. a,b+8,c − c. geom. Dobrze wywnioskowałem ?

ICSP:

jakubs: Dzięki walczę dalej

Hajtowy: Jak już wyliczysz to sprawdź wynik: https://matematykaszkolna.pl/strona/3400.html

jakubs: Podobne zadanko Wyliczyłem i mam poprawne odpowiedzi.

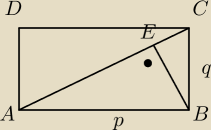
jakubs: Teraz prostokąt W prostokącie ABCD dane są |AB|=p, |BC|=q i p>q. Odcinek BE jest wysokością trójkąta ABC opuszczoną na jego bok AC. Wyraź pole trójkąta ABE za pomocą p i q. Jakaś wskazówka?

jakubs: Pokombinuje jeszcze z podobieństwem trójkątów, może coś się uda.

bezendu: https://matematykaszkolna.pl/forum/246389.html można tylko z pitagorasa

jakubs: Zrobiłem z podobieństwa, ale chętnie zerknę, bo podobieństwa nie lubię

bezendu: To tak jak ja

jakubs: Wielomian W(x)=x⁴−ax³+bx²+12x+9 jest kwadratem wielomianu P(x) =x²+px+q. Oblicz a oraz b . (x²+px+q)²=x⁴+p²q²+q²+2px³+2px²+2pxq Wyznaczam: 2x³p=−ax³ a=−2p bx²=x²(p²+2p) b=p²+2p 12x=2pqx 6=pq q²=9 q=3 ⋁q=−3 A więc będą dwa przypadki kiedy p=2 lub p=−2 a=4 b=0 lub a=−4 b=8 Co robię źle ? W odpowiedziach wyniki a=4 lub a=−4 i odpowiednio b=−2 lub b=10

ICSP: Źle podniosłeś do kwadratu Drugi składnik to p²x² a nie p²q²

jakubs: Oj źle przepisałem, ale nadal będzie tak, że: bx²=p²x²+2px² bx²=x²(p²+2p)

jakubs: up?

jakubs: Mam błąd Dzięki ICSP

bezendu: a to zadanie co ja Ci wysłałem ?

jakubs: bezendu chodzi Ci o ten prostokąt ? czy jakieś inne ?

bezendu: prostokąt

jakubs: Poddałem się, bo nie wiedziałem jak wyznaczyłeś odcinek AE

bezendu: Mogę zrobić to zadanie za 15 minut

jakubs: Ok ja też zaraz spróbuję jeszcze raz

jakubs: Ja raczej nie wymyślę nic, jak możesz bezendu to pokaż jak wyznaczyłeś AE.

bezendu: chwilka już pisze

jakubs: OK super

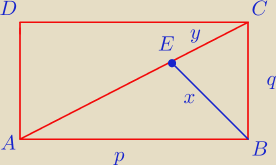
bezendu: |AC|=√p²+q²

	pq
PΔABC=
	2

1		pq
	*x*√p2+q2=		/2
2		2

x√p²+q²=pq x=U{pq}{√p²+q² y²=q²−x²

	pq
y2=q2−(		)2
	√p2+q2

	p2q2
y2=q2−
	p2+q2

	q4
y2=
	p2+q2

	q2
y=
	√p2+q2

	1		pq
PΔABE=		*U[p2}{√p2+q2}*
	2		√p2+q2

	pq3
P=
	2(p2+q2)

jakubs: Dzięki Teraz już rozumiem co i jak.

bezendu:

jakubs: Teraz uderzam w kimę, jeszcze raz dzięki za pomoc. Dobranoc

bezendu: Dzień dobry. Jeszcze 40 zdań z brył