kombinatoryka
tyu: czy ktoś mógłby mi powiedzieć jak czy dobrze liczę to zadanie
Ze zbioru {1,2,3,...,30} losujemy kolejno ze zwracaniem dwie liczby. Oznaczamy je w kolejności
losowania, a i b. Ile jest możliwości
wylosowania takiej pary liczb, dla której 5<
√ (a−b)2 ≤ 10
Liczę to tak 5< Ia−bI ≤ 10
zatem Ia−bI > 5 => a−b >5 i a−b< −5 => a−b ∊ (−
∞; −5) ∪ (5; +
∞) ale tutaj już chyba coś źle
liczę
więc już drugiej nierówności nie mam co rozpisywać. Wie ktoś ja to zrobić.
Tutaj
https://matematykaszkolna.pl/forum/225425.html jest podobne zadanie,
tylko że tam jest
plus pomiędzy a oraz b, a tutaj jest minus, oraz wyrażenie pod
pierwiastkiem jest mniejsze od 10, a tutaj jest
≤.
27 kwi 10:26
mietek: |a−b|>5 ⇔ (a−b>5) ∨ (a−b<−5)
27 kwi 10:38
tyu: ale Twoja uwaga nie wiele mi nie pomaga, bo i tak rozpisanie tego modułu będzie wyglądać tak
samo, czyli a−b ∊ (−∞; −5) ∪ (5; +∞) − o ile się nie mylę.
27 kwi 10:46
mietek: potwierdziłem, że jest ok
27 kwi 10:48
Tadeusz:
Liczę to tak 5< Ia−bI ≤ 10
zatem Ia−bI > 5 => a−b >5 i a−b< −5
tu nie możesz pisać i tylko lub
27 kwi 10:53
tyu: rozpisałem sobie drugi moduł
Ia−bI≤10 ⇔ a−b≤10 i a−b≥10, zatem przedział łącznie z pierwszym modułem będzie taki
(a−b) ∊ ≤−10, 5) ∪ (5, 10≥ i co dalej z tym robić?
27 kwi 10:57
tyu: ok, nie chcę się spierać z Wami, bo przypuszczam, że jesteście ode mnie lepsi z matmy, ale w
książce jest taki zapis
IwI > a ⇔ (w < −a ⋁ w > a) ⇔ w ∊ (−∞, −a) ∪ (a, +∞)
więc napisałem, że to i tak mi nic nie zmienia, jeśli ostateczny nawias wygląda tak
a−b ∊ (−∞; −5) ∪ (5; +∞)
27 kwi 11:03
Tadeusz:
niewiele zrozumiałeś z rozpisywania modułów
27 kwi 11:08
Tadeusz:
|a−b|>5 prowadzi do a−b<−5 lub czyli ⋁ a−b>5
|a−b|≤10 a−b≥−10 i czyli ⋀ a−b≤10
27 kwi 11:12
Tadeusz:
... i teraz poszukaj przedziału/przedziałów wspólnych
(bo masz do czynienia z układem nierówności)
27 kwi 11:14
tyu: przecież napisałem wspólny przedział (a−b) ∊ <−10, 5) ∪ (5, 10> ale nie wiem, co mam z tym
zrobić.
∧ jest w przypadku IwI ≤ a oraz IwI < a
⋁ jest w przypadku IwI ≥ a oraz IwI > a
27 kwi 11:20
27 kwi 11:20
tyu: wiem, ja sobie taki wykres w zeszycie zrobiłem,
27 kwi 11:21
tyu: 
∊ <−10, 5) ∪ (5, 10> chyba to jest prawidłowe odczytanie
układu nierówności
27 kwi 11:24
Tadeusz:
... to teraz szukaj w swoim zbiorze takich par, które spełniają te warunki
27 kwi 11:25
tyu: 
∊ ∊ <−10,
−5) ∪ (5, 10> błąd zauważyłem, brak minusa przy 5 w pierwszym nawiasie
proszę o napisanie jak się szuka takich par − np dwóch pierwszych, bo ja tylko z tego rozumiem,
że a−b mogą się równać dziesięć, ale jak to policzyć ?
27 kwi 11:29
Tadeusz:
Twoje

czyli a−b ma się zawierać w tych przedziałach ... to wypisuj ...
27 kwi 11:43
tyu: chodzi mi po pokazanie dwóch przykładów − jak się je liczy − to chyba nie jest dużo? gdybym to
wiedział, bo bym nikogo nie prosił o pomoc i sam to zrobił, i zaczął rozwiązywać następne
zadania.
27 kwi 11:52
PW: Czy ułatwiłoby życie takie spojrzenie?
− Dla każdej dwójki różnych liczb a, b z podanego zbioru mamy dokładnie dwie możliwości − albo
a > b, albo a < b.
Policzmy więc połowę możliwości − te, dla których a > b. Nie będzie żadnego kłopotu z tymi
cholernymi modułami.
27 kwi 14:10
tyu: no nie policzę

Kombinatoryki i całego rachunku prawdopodobieństwa uczę się sam, bez nauczyciela, więc gdybym
stawał na rzęsach, to nie wiem jak to policzyć. Wszystkie zadania z rach prawdob. staram się
"przełożyć" na wzory permutacji, kombinacji, wariacji, ale w tym zadaniu jakoś nie wiem jak to
policzyć.
Pocieszające jest w tym wszystkim to, że przedwczoraj zauważyłem, że z niektórymi zadaniami, z
którymi ja mam problem, inni też mieli problemy. Nie będę wymieniał nicków, ale te osoby
pomagają teraz innym.
27 kwi 14:33
tyu: wniosek z tego taki, że czyli ci lepsi ode mnie też mieli z tymi zadaniami problem
27 kwi 14:35
PW: Spróbuj po prostu zacząć wypisywać te pary (a,b), dla których a>b i jednocześnie 5 < a−b ≤ 10.
Nikt nie broni powiedzieć:
− Wypisałem wszystkie, jest ich jak widać ...
A może w trakcie wypisywania wpadniesz na pomysł − jak to opisać słowami i policzyć, bez
wypisywania wszystkich par.
27 kwi 14:40
PW: Wniosek też taki: nie ma ludzi, którzy rozwiążą każdy problem, zwłaszcza ot, tak, na
pstryknięcie palcem. To tylko nudne typowe zadania można w ten sposób. To jest nie
nadzwyczajnie trudne, ale nie podpada pod żaden schemat typu "wariacje − kombinacje".
27 kwi 14:43
tyu: dokończę zadanie, które teraz robię, i wracam do tego, o którym tu mowa
27 kwi 14:44
tyu: czy te pary liczb to np
(1,7) bo a=1, b=7, czyli a−b = −6
(1,8) bo a=1, b=8, czyli a−b = −7
(1,9) bo a=1, b=9, czyli a−b = −8
Nie wiem, czy to tak należy liczyć?
27 kwi 17:16
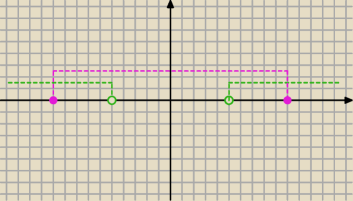 Eta Twoje a−b określiłaby jako
Eta Twoje a−b określiłaby jako  Już wiesz, gdzie jest Twoje
Już wiesz, gdzie jest Twoje 
 −
−
 ∊ <−10, 5) ∪ (5, 10> chyba to jest prawidłowe odczytanie układu nierówności
∊ <−10, 5) ∪ (5, 10> chyba to jest prawidłowe odczytanie układu nierówności
 ∊ ∊ <−10, −5) ∪ (5, 10> błąd zauważyłem, brak minusa przy 5 w pierwszym nawiasie
proszę o napisanie jak się szuka takich par − np dwóch pierwszych, bo ja tylko z tego rozumiem,
że a−b mogą się równać dziesięć, ale jak to policzyć ?
∊ ∊ <−10, −5) ∪ (5, 10> błąd zauważyłem, brak minusa przy 5 w pierwszym nawiasie
proszę o napisanie jak się szuka takich par − np dwóch pierwszych, bo ja tylko z tego rozumiem,
że a−b mogą się równać dziesięć, ale jak to policzyć ?
 czyli a−b ma się zawierać w tych przedziałach ... to wypisuj ...
czyli a−b ma się zawierać w tych przedziałach ... to wypisuj ...
 Kombinatoryki i całego rachunku prawdopodobieństwa uczę się sam, bez nauczyciela, więc gdybym
stawał na rzęsach, to nie wiem jak to policzyć. Wszystkie zadania z rach prawdob. staram się
"przełożyć" na wzory permutacji, kombinacji, wariacji, ale w tym zadaniu jakoś nie wiem jak to
policzyć.
Pocieszające jest w tym wszystkim to, że przedwczoraj zauważyłem, że z niektórymi zadaniami, z
którymi ja mam problem, inni też mieli problemy. Nie będę wymieniał nicków, ale te osoby
pomagają teraz innym.
Kombinatoryki i całego rachunku prawdopodobieństwa uczę się sam, bez nauczyciela, więc gdybym
stawał na rzęsach, to nie wiem jak to policzyć. Wszystkie zadania z rach prawdob. staram się
"przełożyć" na wzory permutacji, kombinacji, wariacji, ale w tym zadaniu jakoś nie wiem jak to
policzyć.
Pocieszające jest w tym wszystkim to, że przedwczoraj zauważyłem, że z niektórymi zadaniami, z
którymi ja mam problem, inni też mieli problemy. Nie będę wymieniał nicków, ale te osoby
pomagają teraz innym.