matma

matma kyrtap: Jak oceniacie dzisiejszą maturę z zadań info. ?

26 kwi 14:13

Marcin: o, zaraz sobie zrobię emotka

26 kwi 14:14

Piotr 10: Trudna.

26 kwi 14:14

kyrtap: Też mi się tak zdaje odnośnie tego ostrosłupa strasznie duże liczby mi wyszły i rzuciłem to zadanie w cholerę

26 kwi 14:15

Piotr 10: z ostroslupem to łatwe, tam trzeba sie nie pomylic w oznaczeniu bok IACI to krawedz podstawy a zrobiles to z trygonometrii ?

26 kwi 14:16

kyrtap: tak czekaj luknę

26 kwi 14:17

kyrtap: czekaj już wiem gdzie błąd o ja dlatego sinus taki wyszedł dziwny już to robię dzięki Piotrze

26 kwi 14:18

kyrtap: poprawiam znaczy

26 kwi 14:19

Piotr 10: a masz ten dowod trygonometryczny zrobiony moze ?

26 kwi 14:19

kyrtap: prawdopodobieństwo za to chyba proste, albo ja źle obliczyłem

26 kwi 14:19

kyrtap: nie wyszedłem z założenia ze α + β + γ = 180 stopni i potem to sinusowałem i z cosinusowałem ale coś nie wychodzi

26 kwi 14:20

kyrtap: chyba że to niepoprawna metoda

26 kwi 14:21

Piotr 10: moment, moze cos wyjdzie teraz mi

26 kwi 14:23

Marcin: Tak jak sobie patrzę na tą maturkę, to nie wydaje się jakaś nadzwyczaj trudna, ale muszę jeszcze ją na spokojnie przerobić emotka

Z tym dowodem trygonometrycznym jednak miałbym problem.

26 kwi 14:23

kyrtap: po 3 pierwszych zadaniach też takie miałem Marcin wrażenie

26 kwi 14:24

Piotr 10: Ja tak samo

piona

26 kwi 14:24

Marcin: Bo czwarte to akurat ten dowodzik

26 kwi 14:25

kyrtap: Piotr 10 jak coś ciekawego Tobie wyjdzie daj znać

26 kwi 14:25

kyrtap: Piotrze podaj wynik jaki Tobie wyszedł w prawdopodobieństwie

26 kwi 14:25

Piotr 10: ile z prostokatem Ci wyszlo ?

26 kwi 14:26

kyrtap: Nie wyszło, liczyłem z tw. cosinusów dla ΔABE niewiadomą x i przyjąłem za α = 45 stopni i potem wyszło mi równanie gdzie Δ jest ujemna pozdro emotka

26 kwi 14:28

Piotr 10: mi wyszlo P= 14√1345 nie mozesz przyjac kata 45⁰, bo nie wiadomo czy to kwadrat

26 kwi 14:29

kyrtap: masz rację

26 kwi 14:31

kyrtap: pomyślę jeszcze bo wydaję się być proste

26 kwi 14:32

Piotr 10: mi sie wydaje ze z tym dowodem z trygonometrii to trzeba te wzory zastosowac

	α+β		α − β
sinα+sinβ = 2 sin		cos
	2		2

26 kwi 14:32

Piotr 10: dobra wiem juz

26 kwi 14:34

Piotr 10: no wg mnie te zadanie wykracza poza program, bo tych wzorow juz nie ma w liceum ale no dobra

26 kwi 14:35

kyrtap: co to za wzór?

26 kwi 14:35

Marcin: Piotrek, a znałeś ten wzór? emotka

26 kwi 14:36

Piotr 10: No znalem bo go stosowalem pare razy tutaj jest https://matematykaszkolna.pl/strona/3670.html

26 kwi 14:37

Marcin: kyrtap, poczytaj sobie tu: http://www.matematyka.pl/2514.htm

26 kwi 14:37

kyrtap: fajnie że te wzory są w tablicach na maturze

26 kwi 14:37

kyrtap: dzięki poczytam emotka

26 kwi 14:38

kyrtap: czyli wniosek z tego taki że nie będę dobrze przygotowany do matury z matmy

26 kwi 14:43

Piotr 10: Spoko, takiego zadania nie powinno byc na naszej maturze raczej

26 kwi 14:43

kyrtap: no ale wiesz jak robię błędnie zadanie z tym prostokątem lub bryłą, szkoda gadać

26 kwi 14:44

Marcin: Jak Ci kilka punktów ucieknie to jeszcze nic takiego strasznego się nie stanie emotka

Przecież nie chcesz mieć 100%

26 kwi 14:50

kyrtap: czemu nie?

Przecież każdy kto się przygotowywał przez trzy lata walczy o 100%

26 kwi 14:51

Piotr 10: Zad.

	α		β		γ
sinα+sinβ+sinγ = 4 cos		*cos		cos
	2		2		2

Rozwiązanie:

	α+β		α−β
sinα+sinβ+sinγ = 2sin		cos		+ sinγ
	2		2

γ=180⁰ − (α+β) ; sinγ=sin(α+β)

	α+β		α−β
2sin		cos		+ sin(α+β)
	2		2

sin2α=2sinαcosα,a więc :

	α+β		α+β
sin(α+β) = 2 sin		* cos
	2		2

	α+β		α−β		α+β		α+β
2sin		cos		+ 2 sin		* cos		=
	2		2		2		2

	α+β		α−β		α+β
=2sin		[ cos		+cos		]
	2		2		2

α+β+γ=180⁰ α+β = 180⁰ − γ

	180⁰ − γ		α−β		α+β
2sin		[ cos		+cos		]
	2		2		2

	α−β		α		β		α		β
cos		= cos		*cos		+ sin		*sin
	2		2		2		2		2

	α+β		α		β		α		β
cos		= cos		*cos		− sin		*sin
	2		2		2		2		2

	α−β		α+β		α		β
cos		+cos		= 2 cos		*cos
	2		2		2		2

A zatem:

	180⁰ − γ		α		β
2sin		* 2 cos		*cos		=
	2		2		2

γ

α

β

γ

α

β

2 * sin ( 900 − 

 ) * 2 cos

*cos

= 2* cos

 * 2 cos

*cos

2

2

2

2

2

2

	α		β		γ
= 4 cos		*cos		cos		( L_s=P_s)
	2		2		2

c.n.w

26 kwi 14:57

kyrtap: najfajniejsze jest to że dużo dają miejsca na maturze do pisania, jeżeli się coś nie powiedzie i się skreśli to już w ogóle miejsca sporo będę miał

26 kwi 14:58

kyrtap: dzięki Piotrze

26 kwi 15:06

Piotr 10: emotka

26 kwi 15:07

kyrtap: lecę coś zjeść bo aż zgłodniałem po tej maturze

26 kwi 15:09

zawodus: Zadanko znane emotka

Jeśli rzeczywiście nie idzie inaczej jak z tego wzoru to wykracza poza materiał. Zaraz pomyśle o innym sposobie emotka

26 kwi 15:14

Piotr 10: Nie da rady inaczej chyba ; / po po prawej stronie są kąty połowkowe wiec trzeba to jakos zastosowac chyba

26 kwi 15:15

himruin: W 5 wyszło mi P=840, a Wam?

26 kwi 19:41

Marcin: Tak. Mi też wyszło P=840.

26 kwi 20:18

matma : i jak Marcin? jakie refleksje?

26 kwi 20:22

kyrtap: kurde zły sobie nick dałem

26 kwi 20:22

Marcin: Na temat tej matury? emotka

W maju będzie na pewno prościej

26 kwi 20:23

Marcin: No mogłem się domyślić że to Ty

Widzę że nicki sobie zmieniasz cwaniaku

26 kwi 20:23

kyrtap: ciągle tak piszesz nie chce mi się wierzyć

26 kwi 20:23

Marcin: Ciągle tak piszę żebyś w końcu uwierzył

26 kwi 20:25

kyrtap: oprócz dzisiejszej matury coś dzisiaj robiłeś z matmy?

26 kwi 20:27

Marcin: Nie. Czekam na nockę emotka

26 kwi 20:28

kyrtap: dobry

26 kwi 20:28

kyrtap: jak tam zakończenie? bo ja wróciłem o 4 rano

26 kwi 20:29

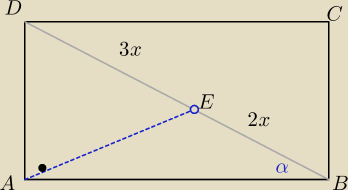
Marcin: rysunek

W tym zadaniu zastosowałem twierdzenie cosinusów emotka

cosα miałem z trójkąta prostokątnego ABD emotka

26 kwi 20:29

Marcin: Ja też chyba jakoś tak, w sumie to nie pamiętam

26 kwi 20:30

kyrtap: zrobiłem to jak mnie Piotr poprawił

26 kwi 20:30

5-latek: To juz jest noc (u mnie za oknem ciemno juz jest wic na poczatek takie Nie wiem czy piszecie podstawe czy rozszerzenie ale macie Rozwiaz rownanie √2log(−x)=log√x²

26 kwi 20:31

Marcin: No to się cieszę!

Załóż zaraz temat, może nam ktoś jakieś fajne zadanko rzuci emotka

26 kwi 20:31

kyrtap: Ja podstawową Marcin rozszerzenie emotka

26 kwi 20:32

kyrtap: już mamy zadanie

26 kwi 20:32

Marcin: 5−latek czytasz w moich myślach

Dzięki za zadanko emotka

26 kwi 20:32

kyrtap: Chyba w moich

26 kwi 20:33

kyrtap: nie jestem pewny odp mogę pisać? emotka

26 kwi 20:36

5-latek: emotka

Ale uwazajcie przy nim

26 kwi 20:37

kyrtap: 1?

26 kwi 20:37

Marcin: Szybciej już −1 emotka

26 kwi 20:39

5-latek: TO jest jedno rozwiaznie . jest jeszce drugie . No to piszczcie rozwiazanie .

26 kwi 20:41

kyrtap: Marcin Tobie wyszło −1?

26 kwi 20:41

kyrtap: Nie może chyba drugie wyjść bo nie jest zgodne z dziedziną?

26 kwi 20:42

Marcin: No według mnie nie możesz wstawić 1, to będzie wtedy log(−1), a to przecież niemożliwe emotka

26 kwi 20:44

5-latek: Rownanie mozesz rozwiazac i sprawdzic rozwiazanie na koncu . Gorzej jest z nierownoscia

26 kwi 20:45

zawodus: I jak wam idzie?

26 kwi 20:47

kyrtap: ok dobra zgadza się

26 kwi 20:49

5-latek: Co mozemy wnioskowac o x z lewej strony rownania . Jakie musi byc ? Wobec tego √x²=|x|= ile ?

26 kwi 20:49

kyrtap: nie kumam już emotka

26 kwi 20:54

Marcin: Ja wywnioskowałem, że x musi być ujemny emotka

Można coś tak kombinować: 2log(−x)=(log√|x|)² Nigdy nie podnosiłem logarytmu do kwadratu, serio emotka

26 kwi 20:55

kyrtap: ja też jak już coś to tam wychodziła jakaś czysta liczba

26 kwi 20:56

Marcin: 2log(−x)=(log|x|)² tzn tak (bez pierwiastka)

26 kwi 20:56

5-latek: Powiem Ci ze to jest troche trudne zadanie . Poczekajmy troche na Marcina moze cos wymysli

26 kwi 20:56

Marcin: Nie wymyślę emotka

26 kwi 20:57

5-latek: Marcin lewa strona prawidlowo natomiast prawa to √x²=|x|=−x pomysl sam dlaczego Wiec dostaniemy rownanie √2log(−x)=log(−x)

26 kwi 21:00

5-latek: podstaw teraz sobie za log(−x)=t i podnies obie strony rownania do kwadratu

26 kwi 21:09

Marcin: log(−x)=(log(−x))² log(−x)=2log(−x) a tak można?

26 kwi 21:12

kyrtap: dziwne to

26 kwi 21:16

Marcin: t=0 t=1 log1=log(−x) −x=1 x=−1 i log10=log(−x) −x=10 x=−10, ok?

26 kwi 21:19

Piotr 10: Macie ode mnie Dane są dwa okręgi o równaniach K₁: (x−3)²+(y+4)²=9 i K₂: x²+y² −18x −8y+96=0. Napisz równanie okręgu o najmniejszym promieniu stycznego zewnętrzenie do danych okręgów.

26 kwi 21:19

5-latek: To sprobuj tak zrobic Ale zauwaz ze jesli za log(−x)=t i obustronnie do kwadratu to dostaniemy t²−2t=0 wiec t₁=0 lub t₂=2 wiec log(−x)=0 to x₁= ile ? lub log(−x)=2 to x₂= ile ?

26 kwi 21:22

Marcin: fakt, omyłkowo podstawiłem 1 i 0 zamiast 2 i 0 Odpowiedzi to −1 i −100, prawda emotka

26 kwi 21:27

5-latek: Teraz proszse rozwiazywac zadanie od kolegi Piotra 10 Ja jutro znajde jakies ciekawe zadanko dla Was To na razie emotka

26 kwi 21:29

5-latek: Tak Marcin emotka

czy bylo latwe ? Tak bylo latwe

26 kwi 21:30

Marcin: hehe ok emotka

26 kwi 21:31

bezendu: Czy Wam też już nic się nie chcę ?

26 kwi 21:31

kyrtap: tak mi tak już od 2 tyg

26 kwi 21:32

bezendu: Czyli nie jestem sam emotka

Brak motywacji co nie ?

26 kwi 21:32

Piotr 10: Tak samo mam, w przyszłym tygodniu to już sam relaks został + język polski i tyle

26 kwi 21:33

Marcin: Bo sobie wkręcacie tą maturę emotka

Ja sobie na luzie z browarkiem trzaskam zadanka i leci

26 kwi 21:33

kyrtap: Polski buahahahaha

26 kwi 21:34

Marcin: Ponoć lepiej na kilka dni przed maturą odstawić naukę. Tak żeby mieć 'świeży' mózg

26 kwi 21:34

Piotr 10: Marcin nie ponoć, tylko trzeba tak zrobić emotka

26 kwi 21:34

bezendu: Taa.. język polski już opanowany emotka

a co do planimetrii to już nawet nie chcę mi się otwierać zeszytu, żeby coś liczyć.

26 kwi 21:35

kyrtap: bezendu co będzie to będzie jeżeli przykładowo ja nie napiszę dobrze podejdę za rok i tyle, świat się nie zawali chyba co nie?

26 kwi 21:36

Marcin: A po maturze nie będziecie wiedzieć co ze sobą zrobić

Tyle czasu będzie że szok emotka

26 kwi 21:36

kyrtap: matura to tylko wynik , nie świadczy zawsze o zdobytej wiedzy

26 kwi 21:36

bezendu: Za rok to trochę boli, ja chodziłem do technikum więc już rok i tak jestem do tyłu co do moich rówieśników emotka

26 kwi 21:37

Piotr 10: Marcin o to bym się raczej nie bał.

. Jeźdzenie po całej Polsce i meczyki w Gdańsku, Krakowie itd

26 kwi 21:37

kyrtap: Ja się zastanawiam jeszcze za rok czy nie zdać sobie tej fizyki rozszerzonej

26 kwi 21:38

Marcin: Słyszałeś o Villanovie?

26 kwi 21:38

Piotr 10: Tak. Niestety, [*].

26 kwi 21:38

bezendu: ?

26 kwi 21:39

kyrtap: ej nie róbmy może dzisiaj zadań co? pogadajmy

26 kwi 21:39

Marcin: kyrtap Ty i tak cały czas tu konwersacje prowadzisz

26 kwi 21:40

kyrtap: wiem

26 kwi 21:41

Piotr 10: O ktorej godz piszemy matme

o 9 ?

26 kwi 21:41

kyrtap: chyba tak

26 kwi 21:41

kyrtap: Marcin już taki jestem lubię gadać, pisać

26 kwi 21:42

Marcin: rozszerzenie tak samo? emotka

26 kwi 21:42

Marcin: Gadać pisać, pić

26 kwi 21:43

kyrtap: to też emotka

26 kwi 21:45

Marcin: To byśmy się dogadali na studiach

26 kwi 21:49

kyrtap: Powiedzcie lepiej na co chcecie się dostać ? w sensie jaki kierunek

26 kwi 21:49

kyrtap: No na pewno

26 kwi 21:49

kyrtap: Niewykluczone że się spotkamy, wszystko jest możliwe

26 kwi 21:50

Marcin: Informatyka stosowana na AGH, tam mam przynajmniej szansę się dostać emotka

26 kwi 21:52

kyrtap: Ja myślałem nad elektrotechniką ale tam chyba fiza jest brana

26 kwi 21:54

kyrtap: Piotrze jesteś?

26 kwi 21:55

kyrtap: trochę jestem zły na siebie

26 kwi 21:57

Marcin: why? emotka

26 kwi 21:59

kyrtap: bo się nie uczyłem fizy wcześniej a spoko jest

26 kwi 21:59

Marcin: fizyka jest spoko? wolę matmę emotka

26 kwi 22:01

kyrtap: też wolę matmę ale fiza nie jest zła

26 kwi 22:02

kyrtap: będę musiał jeszcze popatrzeć na te kierunki

26 kwi 22:04

urta: siema emotka

ej co to za nocki matematyczne? emotka

26 kwi 22:04

bezendu: @urta wszystkiego dowiesz się w swoim czasie.

26 kwi 22:06

Marcin: Nocki? Jeszcze jest wcześnie emotka

26 kwi 22:06

kyrtap: a takie rozkminy mamy zawsze

26 kwi 22:06

urta: a można dołączyć?

26 kwi 22:08

kyrtap: głupio się pytasz, pewnie że można

26 kwi 22:09

Marcin:

	33		12
(x−		)²+(y−		)²=9, tak będzie? Bo nigdzie nie sprawdzałem.
	5		15

To jest to zadanie od Piotrka emotka

26 kwi 22:09

urta: to śledzę forum

26 kwi 22:11

Marcin: Urta jak masz jakieś ciekawe zadanka, to wrzucaj je tu emotka

26 kwi 22:12

kyrtap:

	cosx
Rozwiąż równanie 2sin2x +		= 4cosx jeśli x ∊ <0,2π>. Ze zbioru rozwiązań tego
	sinx

równania losujemy bez zwracania dwie liczby. Oblicz prawdopodobieństwo zdarzenia, że co

	π
najmniej jedno z wylosowanych rozwiązań jest wielokrotnością liczby		.
	2

26 kwi 22:17

urta: ja to cieniutki z tej matmy jestem emotka

ale zauważyłem, że fajnie tu u was emotka

zacznę robić te zadanka z matury o której tutaj mowa

a potem się zobaczy

26 kwi 22:17

kyrtap: urta a jesteś w klasie maturalnej czy nie?

26 kwi 22:17

Marcin: Tutaj większość mówi że jest słaba z matmy, a jak przyjdzie co do czego, to tylko ja będę mieć słaby wynik

26 kwi 22:19

urta: ja byłem w klasie maturalnej rok temu, uzyskałem 52% i w tym roku poprawiam, ale nie uczyłem się za dużo i sporo zapomniałem

czuję, że będzie kicha

26 kwi 22:19

urta: ojj nie, na pewno nie

widziałem jakie Wy tam macie rozkminy, głowa mała

26 kwi 22:19

kyrtap: ostatnio aż takich nie ma emotka

26 kwi 22:20

Marcin: Nowy w grupie i już się podlizuje

Popatrz się popatrz

26 kwi 22:21

urta: jaką maturę w tym roku obstawiacie? trudniejszą niż rok temu, czy może na odwrót?

26 kwi 22:21

urta: nie podlizuje! haha

jedynie mogę pozazdrościć

26 kwi 22:21

Marcin: Pewnie że łatwiejszą emotka

26 kwi 22:21

kyrtap: Ja zdaję podstawową więc ludzie mówią że będzie prosta

26 kwi 22:22

Marcin: Chłopak zaczynał od rozszerzonej fizyki, teraz już tylko matma podstawowa, a do matury jeszcze jest trochę czasu. Pewnie się jeszcze wypiszesz, nie?

26 kwi 22:24

kyrtap: nom

26 kwi 22:24

kyrtap: a ile to roboty?

26 kwi 22:24

urta: haah

robicie to zadanko ? bo ja prawie już rozwiązałem równanie

26 kwi 22:25

Marcin: Jakie zadanko? emotka

26 kwi 22:26

kyrtap: Które dałem?

26 kwi 22:27

urta: krytap wstawił o godzinie 22:17

26 kwi 22:28

Marcin: Ty faktycznie. Nie zauważyłem

26 kwi 22:28

urta: z tego równania mi wyszło:

	π		5π
x=		∪ x=
	6		6

26 kwi 22:29

urta: haha, to jak zrobicie, sprawdźcie czy dobrze ja mam

a teraz pokminię 2 część zadanka

26 kwi 22:30

kyrtap: urta a cosx= 0 ?

26 kwi 22:36

Marcin: cosx=0

	√3
cosx=
	2

	√3
cosx=−
	2

26 kwi 22:37

kyrtap: jak wy to liczyliście?

26 kwi 22:37

kyrtap: mi cztery rozwiązania wyszły

26 kwi 22:38

Marcin: a co, źle mam?

26 kwi 22:38

zawodus: Zadanie na dziś

Wyznacza równanie krzywej na której znajdują się wierzchołki paraboli opisanej równaniem (a²+1)x²+(a³+a)x+2a=0, gdzie a należy do R emotka

26 kwi 22:39

kyrtap:

π		π		5		3
	,		,		π i		π
6		2		6		2

26 kwi 22:39

urta: dobra ja coś pogubiłem

26 kwi 22:41

Marcin: No to może się gdzieś walnąłem emotka

26 kwi 22:41

Marcin: dzięki zawodus emotka

26 kwi 22:42

urta: dobra ja już widzę u siebie błąd, chwilka

26 kwi 22:43

kyrtap: na spokojnie urta mamy czas

26 kwi 22:43

Marcin: Ok, też widzę błąd emotka

26 kwi 22:43

kyrtap: na szczęście ja liczę w nocy lepiej

26 kwi 22:44

Marcin: Po wczorajszym mnie jeszcze chyba trzyma

26 kwi 22:45

urta: Ej no nie

teraz mi wyszło tak jak u Marcina emotka

Marcin gdzie jest Twój błąd, bo ja go nie widzę aktualnie

26 kwi 22:46

Marcin: Na samym początku miałem błąd przy mnożeniu. emotka

Nie sprawdzałem drugi raz emotka

26 kwi 22:47

urta: dobra wiem

haha

26 kwi 22:50

urta: w kolejnej części to wiem, że Ω=4 hahaha i tyle mojego chłopaki

26 kwi 22:55

kyrtap: Ω = C²₄

26 kwi 22:56

kyrtap: Ω = 6

26 kwi 22:57

kyrtap: żyjcie

26 kwi 23:02

Marcin:

	5
P(A)=
	6

26 kwi 23:04

Marcin: Ω= 4*3

	2		1		2
P(A')=		*		=
	4		3		12

12		2		10		5
	−		=		=
12		12		12		6

26 kwi 23:06

urta: haha to z prawdopodobieństwa nie wiem w takim razie nic emotka

ale spokojnie! jeszcze dużo czasu do matury

26 kwi 23:07

Hajtowy: Marcin szykuj 0,7 xD

26 kwi 23:08

Marcin: Już leży u mnie, zmrożona <3

26 kwi 23:09

kyrtap: Marcin inny sposób ale wynik ten sam

26 kwi 23:09

kyrtap: 0,7 też wypije

26 kwi 23:09

Marcin: Ty to wiadomo, nawet nie pytam

26 kwi 23:11

kyrtap: żebyś Marcin nie myślał że ja alkoholik emotka

26 kwi 23:15

Marcin: Żartuję przecież emotka

Masz tam jakieś zadanie?

26 kwi 23:16

kyrtap: tak mam

26 kwi 23:20

Marcin: No to na co czekasz? Pochwal sie emotka

26 kwi 23:21

kyrtap:

	2m +1
Dla jakich wartości parametru m równanie sin⁴x + cos⁴x =		ma rozwiązanie?
	m−1

26 kwi 23:23

Marcin: rysunek

Potrzeba wykres sin⁴x+cos⁴x i później pozioma kreska emotka

26 kwi 23:26

kyrtap: niekoniecznie w tym wypadku trzeba rysować wykres

26 kwi 23:28

kyrtap: i tak w ogóle jak narysujesz taki wykres bo ja takiego nigdy nie rysowałem

26 kwi 23:28

Marcin: sin⁴x+cos⁴x= (sin²x+sin²x)² − 2sin²xcos²x

26 kwi 23:29

kyrtap: ja jak mam sinusy i cosinusy to szacuję zbiór wartości

26 kwi 23:29

Marcin: Jak to szacujesz?

26 kwi 23:31

Marcin:

2m+1		1
	≥
m−1		2

2m+1
	≤1
m−1

To trzeba rozwiązać. Część wspólna to będzie rozwiązanie.

26 kwi 23:34

kyrtap:

	1
(sin²x+cos²x)² − 2sin²xcos²x = 1− 2(		sin2x)²
	2

26 kwi 23:35

Marcin:

	1
No i jak z tego stwierdzisz, że m∊<		;1>?
	2

26 kwi 23:38

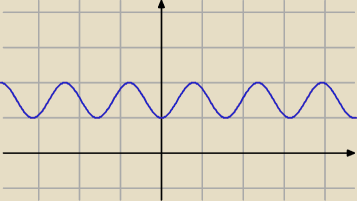
Marcin: rysunek

To będzie coś takiego emotka

26 kwi 23:40

kyrtap: myślałem że swoim sposobem zrobię ale nie wychodzi mi zgodnie z odp czekaj jeszcze chwilę pomyślę

26 kwi 23:42

kyrtap: bo tylko mam odp do zadań a rozwiązań nie

26 kwi 23:42

kyrtap: dobra już piszę wyszło

26 kwi 23:44

Marcin: Jak wyszło ok się cieszę emotka

Ale dalej nie wiem jak Ty to szacujesz

26 kwi 23:45

kyrtap:

	1		2m+1
1− 2(		sin2x)² =
	2		m−1

	1		2m+1
1 − 2 *		sin²x =
	4		m−1

	1		m+2		1
−		sin²x =		/:(−		)
	2		m−1		2

	−2m −4
sin²x =
	m−1

−1≤sin2x≤1 0≤sin²x≤1

	−2m−4
0 ≤		≤1
	m−1

26 kwi 23:51

kyrtap: w przedostatnim sin² 2x

26 kwi 23:52

Marcin: https://www.wolframalpha.com/input/?i=sin%5E4x%2Bcos%5E4x Zobacz sobie wykres. Nie może być tak jak Ty masz.

26 kwi 23:56

kyrtap: nie wiem jak tak zawsze wyznaczałem zbiór wartości niech ktoś moje rozwiązanie zweryfikuje jak może

27 kwi 00:02

kyrtap: ja*

27 kwi 00:02

kinia: @kyrtap ...... jest ok emotka

dokończ ..... rozwiąż tę nierówność podwójną ( i założenie m≠ 1

27 kwi 00:06

bezendu: o i Eta się znalazła

27 kwi 00:09

kyrtap: m∊<−2 , −1>

27 kwi 00:12

kinia: emotka

27 kwi 00:12

kyrtap: kinia = Eta tak?

27 kwi 00:12

kinia: ok emotka

27 kwi 00:12

bezendu: kinia=kinia Nie wiesz o co chodzi kyrtap, więc niech lepiej tak zostanie emotka

27 kwi 00:13

kyrtap: oki nie wnikam

27 kwi 00:13

kinia: emotka

Ważne,że podałeś poprawną odp

27 kwi 00:14

kyrtap: Marcin zaciąłeś się jak płyta

jesteś?

27 kwi 00:17

kinia: Pewnie za dużo było "browarku"......... emotka

27 kwi 00:18

Marcin: No jeszcze żyję emotka

Klawiatura mi zwariowała i nie wiem co się dzieje

27 kwi 00:19

Marcin: Dzisiaj nie, wczoraj tak. Cześć Eta emotka

27 kwi 00:20

kinia: emotka

27 kwi 00:20

kyrtap:

27 kwi 00:35

bezendu: ?

27 kwi 00:36

Marcin: Cisza się zrobiła, wszyscy robią zadania, Eta nie ma komu pomagać emotka

27 kwi 00:38

jakubs: Ja tam zadanek nie robię, dzisiaj cały dzień kaca leczyłem

27 kwi 00:53

kyrtap: Marcin jakieś newsy?

27 kwi 00:53

Marcin: A jakie chcesz newsy? emotka

Jakubus i po co Ci było to picie, no po co?

27 kwi 01:00

jakubs: Mało wypiłem, ale rano głupi zamiast coś zjeść napchałem się witaminkami, a później no to już no wiesz można się domyślić

27 kwi 01:06

Marcin: No napychanie się witaminkami było głupim pomysłem

Lepiej przed samym pójściem spać wypić duużo wody emotka

27 kwi 01:11

jakubs: Jak to mówią Polak mądry po szkodzie

27 kwi 01:22

Marcin: Tylko że to tak zawsze jest emotka

Niby się wie, że się nie powinno pić za dużo, bo na następny dzień będzie męczyć, ale ludzie i tak to robią

27 kwi 01:25

jakubs: Hehe no tak to jest

27 kwi 01:26

Piotr 10: Marcin zadanie z okręgiem emotka

27 kwi 11:37

zawodus: Wczoraj już nie miałem czasu, ale jak ktoś dzisiaj chce to pokażę wam rozwiązanie zadania z trygonometrii bez użycia wzorów na sumę sinusów emotka

27 kwi 12:49

Piotr 10: Jestem bardzo ciekawy,

. Czyżby tw. sinusów ? Ale jak

27 kwi 12:52

Piotr 10: Albo coś na temat tw dwusiecznej kata ?

27 kwi 12:53

zawodus: Nic takiego emotka

proste wzorki emotka

Za parę minut wrzucę emotka

Twierdzenie sinusów mówi o bokach, a tutaj ich nie mamy emotka

27 kwi 12:53

Piotr 10: Ok czekam,

27 kwi 12:54

zawodus: Jeszcze chwila bo muszę ziemniaki obrać na obiad

27 kwi 13:06

Piotr 10: Luzik

27 kwi 13:06

zawodus: Jestem emotka

Na początek parę prostych zależności emotka

α+β+γ=π Prawdziwe są następujące wzory: 1. sinγ=sin(π−(α+β))=sin(α+β) 2. sin(α+β)=sinαcosβ+cosαsinβ

	α
3. cosα=2cos²(		)−1
	2

	α+β		γ
4. sin(		)=cos(		)
	2		2

Trzecia zależność jest trochę trudniejsza emotka

Napisz czy wszystko jasne i przystępujemy do dowodu. emotka

27 kwi 13:39

kyrtap: zawodus dawaj dla mnie zrozumiałe

27 kwi 13:46

zawodus: Do wykazania jest równość:

	α		β		γ
sinα+sinβ+sinγ=4cos(		)cos(		)cos(		)
	2		2		2

Rozpiszemy lewą stronę: L=sinα+sinβ+[sinγ]= (1) =sinα+sinβ+[sin(α+β)]= (2) =sinα+sinβ+[sinαcosβ+cosαsinβ]= [sinα](1+cosβ)+[sinβ](1+cosα)= (2)

	α		α		β		β
=[2sin(		)cos(		)]*(1+cosβ)+[2sin(		)cos(		)]*(1+cosα)= (3)
	2		2		2		2

α

α

β

β

β

α

=2sin(

)cos(

)*[2cos2

]+2sin(

)cos(

)*[2cos2

]=

2

2

2

2

2

2

α

β

α

β

β

α

=4cos(

)cos(

)(sin(

)*cos(

)+sin(

)cos(

)) = (4)

2

2

2

2

2

2

	α		β		γ
=4cos(		)cos(		)cos(		)=
	2		2		2

P c.k.d Chciałem pokolorować wykorzystanie wzorów, ale nie do końca się udało emotka

W nawiasach są zaznaczone przejścia wynikające z wzorów podanych powyżej emotka

Niestety, ale pisanie tutaj to dla mnie tragedia emotka

27 kwi 14:12

kyrtap: zawodus zajebisty jestes

27 kwi 14:16

zawodus: Wcale nie

po prostu trochę bardziej doświadczony emotka

Mam nadzieję, że wszystko zrozumiałe emotka

Poczekamy na opinie Piotrka emotka

27 kwi 14:17

Marcin: Nie zrobiłbym tego zadania na maturze, ale i tak dzięki za rozpisanie zawodus emotka

27 kwi 14:19

kyrtap: Ciekawe czy rozpisanie α+β+γ = 180 byłby punkt

27 kwi 14:20

kyrtap: bo chyba za Ω są jakieś punkty w zadaniu z prawdopodobieństwem

27 kwi 14:24

Marcin: Pewnie. Oni za takie głupoty czasem punktują, że lepiej pisać cokolwiek jak się nic nie wie

27 kwi 14:27

kyrtap: np. rozpisać dane

27 kwi 14:29

Marcin: haha no dokładnie

27 kwi 14:29

kyrtap: kiedyś pamiętam na spr nauczycielka za rozpisanie danych dała mi 0,5 pkt

27 kwi 14:30

zawodus: Ocenianie jest za postęp w zadaniu. Napisanie warunku α+β+γ=180 to już pewien postęp emotka

Nie oszukujmy się. To zadanie byłoby wg mnie wykazać w stanie tylko około 5% maturzystów. Zadanie zbyt trudne jak na maturę. Co nie znaczy, że gdyby was uczono 4 lata (dawne liceum), to moglibyście stawiać takim problemom czoła emotka

27 kwi 14:35

Marcin: CKE nie daje takich zadań, mówię wam emotka

27 kwi 14:37

kyrtap: Marcin może bo był w technikum

27 kwi 14:46

Marcin: Ja nawet nie miałem rozszerzonej matmy emotka

27 kwi 14:48

zawodus: Zawsze możesz ją sobie rozszerzyć

27 kwi 14:54

Marcin: właśnie sobie rozszerzam

27 kwi 14:56

kyrtap: Fajnie nie byłeś na rozszerzonej a zapewne wiesz więcej ode mnie

27 kwi 15:12

Marcin: Ja jestem samoukiem, także nieciekawie.

27 kwi 15:20

zawodus: Liczy się zaangażowanie emotka

27 kwi 15:22

bezendu: Liczy się zaangażowanie hmm ciekawe.. Ciekawe czy się sprawdzi to..

27 kwi 15:22

jakubs: Ja chodziłem do mat−fizu i mniej umiem niż wy

27 kwi 15:24

zawodus: i trochę talentu

27 kwi 15:24

kyrtap: u nas wiecznie mówiła nauczycielka że pracą można wszystko, w liceum nie umiała sterometrii ale jak poszła na studia i przerobiła 500 tysięcy zadań to mówi że dla niej to pestka

27 kwi 15:26

Marcin: Jakby liczyło się zaangażowanie, to bezendu mógłby tutaj wszystkich uczyć matmy emotka

27 kwi 15:26

kyrtap: no raczej emotka

27 kwi 15:27

kyrtap: a ja bym Marcin uczył chyba polskiego co?

27 kwi 15:27

Marcin: Co Ty! Fizyki!

27 kwi 15:34

kyrtap: Fizyki za rok mogę

27 kwi 15:35

kyrtap: dobra ja za jakieś zadania się wezmę

27 kwi 15:42

Marcin: Jak coś masz ciekawego to rzucaj, ale już w nowym temacie emotka

Teraz się relaksuję

27 kwi 15:43

kyrtap: dobra jak będę miał to wrzucę

27 kwi 15:45

zombi: Jak zrobić to 9. ze środkową? Ma ktoś wzorcówki z ZI? emotka

Głupia, planimetria ; (

27 kwi 21:55

Eta:

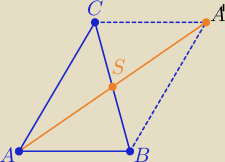
Zbuduj równoległobok : |AB|=|CA^'| , |AC|=|BA^'| i |AA^'|= 2*|AS| teraz z nierówności trójkąta |AB|+|BA^'| > |AA^'| ⇒ ....... teza

27 kwi 22:16

zombi: Łoo jezu, takie coś tylko. Dzięki Eta emotka

Btw. ma ktoś odpowiedź to prawdo?

27 kwi 22:22

kyrtap: 18/77 jak dobrze pamiętam

27 kwi 22:23

Eta:

27 kwi 22:29

zombi: Tyle mi wyszło, dzięki

27 kwi 22:29

kyrtap: luzik emotka

27 kwi 22:29

tomek: Moglby ktos napisać odpowiedzi jakie mu wyszły do kazdego zadania, bo chciałbym sobie sprawdzić czy dobrze zrobiłem?

28 kwi 12:38

razor: napisz swoje to sprawdze

28 kwi 12:39

zawodus: Pracą nie da się wszystkiego osiągnąć emotka

30 kwi 11:13

czarli i fabryka czekolady: pracą da się wszystko osiągnąć

30 kwi 11:13