geometria analityczna analizaaa: Dane są punkty A(−3,2) i B (5,−2). Wyznacz na prostej m: y=−2x+2 taki punkt C, aby trójkąt ABC był prostokątny i odcinek AB był przeciwprostokątną w trójkącie.

domi:

lizak: https://matematykaszkolna.pl/forum/316756.html

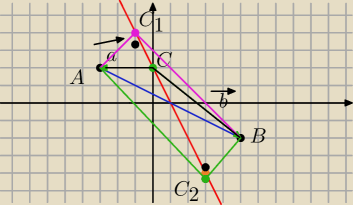
Bo_ra: Punkt C ma wspólrzedne C=(x,−2x+2) Zaznaxczyłem sobie na rysunku tylko dla orientacji obliczen Po oblicxzeniach zrobic poprawke A=(−3,2) B=(5,−2) C=(x,−2x+2) Wektor CA=a→=[x−(−3), −2x+2−2]=[x+3 , −2x] Wektor CB=b→=[x−5, −2x+2−(−2)]=[x−5, −2x+4] Iloczy skalrny wektorów a i b musi równac się 0 a→ob→=0 (x+3)(x−5)+(−2x)(−2x+4)=0 x²−2x−15+4x²−8x=0 5x²−10x−15=0 /(:5) x²−2x−3=0 Δ=16

	2−4
x1=		=−1
	2

	2+4
x2=		=3
	2

Dla x₁=−1 y₁=−2x+2=4 stąd C₁=(−1,4) Dla x₂=3 y₂=−2x+2= −4 stąd C₂=(3,−4)