wyznacz punkt c i oblicz pole trojkata kasialek: Dane są punkty A=(−3,2) oraz B=(5,−2). Wyznacz na prostej y=−2x+2 taki punkt C, aby trójkąt ABC był prostokątny i odcinek AB był przeciwprostokątną w tym trójkącie. Oblicz pole tego trójkąta. Obliczyłam tak : A=(−3,2) B=(5,−2) C=(x,y) y=−2x+2 y= 2−2x C=(x; 2−2x) I AB I=√[(5+3)²+(2+2)²]=√80=4√5 I BCI=√[(5−x)²+(2−2x+2)²]=√[25−10x+x²+16−16x+4x²]=√[5x²−26x+41] IACI=√[(x+3)²+(2−2x−2)²]=√[x²+6x+9+4x²]=√[5x²+6x+9] I I ACI²+I BCI ²=I AB I² 5x²+6x+9+5x²−26x+41=80 10x²−20x+50−80=0 /;10 x²−2x−3=0 Δ=b²−4ac=4+12=16 √Δ=4 x1=[2−4]/2=−1 y1=−2*(−1)+2=4 x2=[2+4]/2=3 y2=−2*3+2=−4 C= (−1,4) v C=(3,−4) i podstawiłam za x aby obliczyć |AC| i |BC| ale pole wychodzi mi źle. Ma byc odpowiedz Pabc1=12 i Pabc2=12 . pomoze ktoś ?

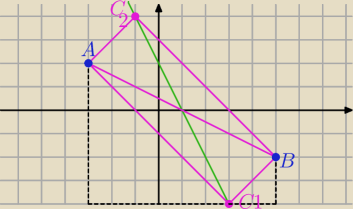
buźka: I dobrze: C₁(3,−4) , C₂(−1,4) |AC₁|=|BC₂|= 6√2 , |BC₁|=|AC₂|=√2 P(ABC₁)= P(ABC₂)= 6√2*√2= 6*2=12 [j²]

kasialek: dziękuję