geometria analityczna Robak: Mógłby mi ktoś wyjaśnić to zadanie okrąg o jest obrazem okręgu o równaniu x²+y²−6x+8y=0 w jednokładności o środku s=(5,2) i skali k=−1,5. znajdź środek i promień okręgu o. No to zaczynam tak, że znajduje promień i współrzędne punktu S S=(3,−4) r=5 r'=5*−1,5=−7,5 Czyli mam już promień drugiego okręgu, ale jak dojść do jego środka? Proszę o podpowiedzi

Robak: tutaj S=(3,−4) jest równe środkowi okręgu, przyzwyczajenie z równania okręgu. S=(3,−4) = O=(3,−4)

daras: wyszukiwarka nie działa https://matematykaszkolna.pl/strona/902.html

Robak: Kiedy ja nie mogę wpaść jak to zrobić.. Widziałem to.

daras: k= −1,5 oznacza jednokładność odwrotną więc jak widziałeś ale czy czytałęś? a jesli przeczytałeś, to czy zrozumiałeś, że okrąg do "góry nogami" będzie po prostu okręgiem o dodatnim promieniu r = + 7,5

daras: środek okręgu będzie leżał na prostej prostopadłej do średnicy w odległości 1,5x wiekszej i po drugiej stronie środka jednokładności S(5,2), a środek okręgu, który masz przekształcić ma współrzędne O(3, −4) dalej już ty...

Mila: x²+y²−6x+8y=0 w jednokładności o środku s=(5,2) i skali k=−1,5. znajdź środek i promień okręgu o. (x−3)²−9+(y+4)²−16=0⇔ (x−3)²+(y+4)²=25 S₁=(3,−4), r=5 S=(5,2) wsp.środka jednokładności

	−3
k=
	2

	−3		15
R=|		|*5=
	2		2

Z definicji jednokładności S₂=(x,y) współrzędne środka nowego okręgu

	−3
SS2→=		*SS1→
	2

SS₁^→[3−5,−4−2]=[−2,−6]

	−3
SS2→=[x−5,y−2]=		*[−2,−6]
	2

x−5=3 y−2=9 x=8 y=11

	15
S2(8,11), R=
	2

Równanie:

	225
(x−8)2+(y−11)2=
	4

Możesz skorzystać z wzoru na wsp. punktu po przekształceniu: S(a,b)=(5,2) środek j. (x,y)=(3,−4) dany punkt x'=k*(x−a)+a y'=k*(y−b)+b

	−3		−3
x'=		*(3−5)+5=		*(−2)+5=3+5=8
	2		2

	−3		−3
y'=		*(−4−2)+2=		*(−6)+2=9+2=11
	2		2

(x',y')=(8,11) wsp. punktu po przekształceniu.

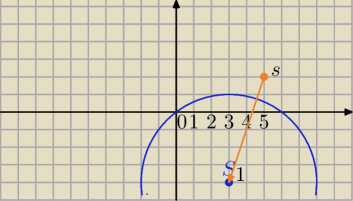
daras: a ja z rysunku znalazłem środek (8,11), w który wbiłem nóżkę cyrkla i zatoczyłem kółeczko o promieniu 7,5

Mila: daras Problem też polega na tym, że uczniowie nie potrafią geometrycznie przekształcać figur.