matma
kyrtap : Gotowi na noc pełną wrażeń?
23 kwi 00:45
Marcin: No ja już mam popcorn

23 kwi 00:46
bezendu:
Proponuje planimetrię

23 kwi 00:46
kyrtap : dobra to dawajcie włączam zegar
23 kwi 00:47
Marcin: W trójkącie ABC proste zawierające dwusieczne kątów poprowadzonych z wierzchołków A i B
przecinają się pod kątem ∘ 45 . Wiedząc, że AC = 2 i BC = 6 , oblicz
−długość boku AB trójkąta ABC ;
−długość środkowej trójkąta ABC poprowadzonej z wierzchołka C .
A łap, pewnie robiłeś

23 kwi 00:48
bezendu:
Na wysokości CD trójkąta ABC wybrano punkt P taki, że |P D | = |P E| , gdzie D i E są
rzutami tego punktu odpowiednio na boki AB i BC . Wiedząc, że tg ∡ABC = 2√2 oblicz iloraz
23 kwi 00:49
kyrtap : to które robimy ?
23 kwi 00:50
bezendu: 2
23 kwi 00:51
Marcin: Ja jeszcze kończę inną maturkę. Zaraz dołączę

23 kwi 00:52
Marcin:
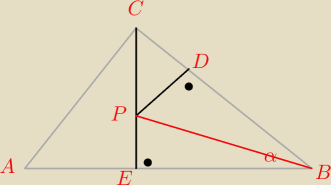
Rysunek będzie chyba mniej więcej jakiś taki

23 kwi 00:58
kyrtap : jak się wpisuje literki w tym rysowniku?
23 kwi 00:59
Marcin: Masz taką literkę T i piszesz

23 kwi 01:00
bezendu:
skąd tam kąty proste ?
23 kwi 01:01
kyrtap : z podobieństwa?
23 kwi 01:01
kyrtap : bo rzut prostokątny
23 kwi 01:02
kyrtap : Marcin te literki powinny być odwrotnie chyba E i D
23 kwi 01:02
Marcin: h=2
√2|EB|,
bezedu próbujesz tam coś?

23 kwi 01:02
Marcin: ahh no tak, odwrotnie

23 kwi 01:03
bezendu:
próbuje ale spać mi się chcę

23 kwi 01:03
kyrtap : strzel sobie kawkę

23 kwi 01:04
5-latek:
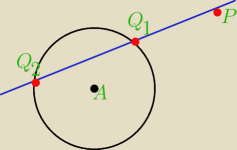
No to macie zadanko na noc pelna wrazen

dany jest okrąg o(A,r) i punkt P .
Udowodnic ze dla kazdej prostej przechodzacej przez P i nierozlacznej z o(A,r) iloczyn
odleglosci punktu P od punktow przeciecia tej prostej z okregiem wynosi |Ap
2−r
2|
23 kwi 01:05
bezendu:
Ja kawy nie pijam

Ale może browar

23 kwi 01:05
5-latek: Ma byc |AP2−r2|
23 kwi 01:06
kyrtap : no browarek też dobry
23 kwi 01:06
5-latek: Bezendu to jest z tego zbioru o ktorym CI wspominalem
23 kwi 01:07
kyrtap : wyszło mi że IEBI = IBDI
23 kwi 01:09
kyrtap : 
23 kwi 01:10
bezendu:
5−latek Ty masz tą książkę udowodnij.. ?
23 kwi 01:10
5-latek: Tak mam ta ksiazke
23 kwi 01:11
Marcin: Jakby tak oznaczyć boki w tym trójkącie:
DB=x
EC=h
CB=q
Too
x
2+(2
√2x)
2=q
2
x
2+8x
2=q
2
9x
2=q
2
3x=q
Oznaczenia już z prawidłowego rysunku

23 kwi 01:11
bezendu:
A masz konto na zadania.info ?
23 kwi 01:12
Marcin: No i chyba dobrze Ci wyszło

Teraz jak już wiemy że są równe, to
|BD|=x
|DC|=2x

23 kwi 01:14
Marcin: Ja mam tam konto, chcesz login i hasło?

23 kwi 01:14
bezendu:
Mam tam login i hasło

23 kwi 01:15
5-latek: mialem ale mi sie skonczylo . Moze w maju zaloze .
napisz co potrzebujesz

23 kwi 01:15
bezendu:
Podaj jaki masz tam login to do Ciebie napisze.

23 kwi 01:15
Marcin: 5−latek kiedyś napisał, że szkoda nam kasy na konto tam, a na piwo mamy. W tym samym dniu
jeszcze kupiłem tam premium

23 kwi 01:16
bezendu:
Nie chodzi mi o abonament bo również posiadam

23 kwi 01:17
Marcin: Mój login? jestem Frings

23 kwi 01:18
kyrtap : Marcin masz wynik?
23 kwi 01:20
bezendu:
5−latka

23 kwi 01:20
23 kwi 01:23
kyrtap : i git

23 kwi 01:23
Marcin: 
23 kwi 01:24
5-latek: Moj login to krzysiek1958
Ale moze napisz jutro albo do 10 albo po 13 a jak nie to dopiero kolo 23 bo od 14 jestem
w pracy OK?
23 kwi 01:25
kyrtap : robimy zadanie 5−latka?
23 kwi 01:25
Marcin: Muszę się nad tym zadaniem głębiej zastanowić. Masz jakiś pomysł?

23 kwi 01:27
bezendu: ok

napisałem również do Fringsa

23 kwi 01:27
Marcin: Czuję się zaszczycony

23 kwi 01:29
5-latek: bede czekal na wiadomosc a tera czas spac

Dobranoc maturzysci
23 kwi 01:29
bezendu:
chyba Cię tam nie znajdę za dużo osób

23 kwi 01:29
kyrtap : bye
23 kwi 01:30
Marcin: Dobranoc

23 kwi 01:30
kyrtap : coś może z wykombinować tw. o stycznej i siecznej czy to głupi pomysł?
23 kwi 01:35
Marcin:
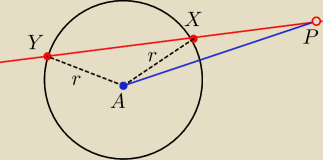
PX*PY=|AP
2−r
2|
Dalej nie macie pomysłów?

23 kwi 01:35
Marcin: Ale tutaj nie ma stycznej

23 kwi 01:37
kyrtap : to dorysujmy? dorysuj marcin i wyświetl jeszcze raz ok niech będzie na dole
23 kwi 01:38
Marcin: Można zapisać coś takiego:
PX*XY=PC*2r
C to punkt przecięcia się prostej PA z okręgiem.
W sumie mało to daje

23 kwi 01:38
Marcin: Chociaż nie można tak jak zapisałem

23 kwi 01:39
kyrtap : dorysuj tą styczną na dole
23 kwi 01:41
kyrtap : to pokombinujemy
23 kwi 01:42
Marcin:
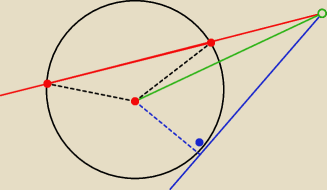
Tak?
23 kwi 01:42
kyrtap : ok daj minutę na przeanalizowanie
23 kwi 01:43
Marcin: Q
2= PX*XY
Q
2=PA
2+r
2 
A miało być troszkę inaczej

23 kwi 01:45
kyrtap : patrz z tw. o odcinkach siecznej i stycznej mamy taki wzór że PX * PY = PO2 gdzie O to ten
wierzchołek na dole okręgu
23 kwi 01:46
Marcin: A nie!
Q
2+r
2=PA
2
Q
2=PA
2−r
2! Genius

23 kwi 01:46
Marcin: Dobra, rozwiązane.

23 kwi 01:47
kyrtap : AO = r
czyli z tw. Pitagorasa mamy
r2 + IOPI2 = IAPI2 ⇒ IOPI2 = IAPI2 −r2
23 kwi 01:49
Marcin: bezendu − ja nie mam uprawnień do pisania wiadomości na zadania.info

23 kwi 01:49
Marcin: wiem, wiem

23 kwi 01:49
kyrtap : dobrze czy źle kombinuje?
23 kwi 01:49
Marcin: Dobrze. Zadanie już zostało rozwiązane

Za chwilę coś innego będziemy robić. A to zadanie to
Twoja zasługa, brawo

23 kwi 01:50
kyrtap : może 50% będę miał z tej matury na koniec
23 kwi 01:51
Marcin: Dane są punkty A (6,− 3),B (1,2) oraz C (2m
3 − 18m ,−m
2) . Wyznacz wszystkie wartości m ,
dla których proste AB i AC są prostopadłe.
Nie ma co myśleć o procentach

23 kwi 01:52
kyrtap : tu chyba coś ze współczynnikami kierunkowymi trzeba będzie pokombinować
23 kwi 01:54
Marcin: Pewnie tak. Już się za to biorę

23 kwi 01:55
kyrtap : pr AB: y = −x − 9 ?
23 kwi 01:56
Hugo: imieniny dzisiaj mam xd Wojciecha

23 kwi 01:57
Marcin: A nie czasem −x+3?

23 kwi 01:58
Marcin: Pogratulować. Stawiasz alko!

23 kwi 01:58
kyrtap : takie równanie wyszło 2m3 + m2 − 18m − 9 = 0 ?
23 kwi 01:59
kyrtap : | | 2 +3 | |
nie wiem ale chyba dobrze liczyłem y +3 = |
| (x−6) |
| | 1−6 | |
23 kwi 02:00
razor: dobrze
23 kwi 02:01
razor: co do równania z m

23 kwi 02:01
kyrtap : m = 3 ⋁ m= −3?
23 kwi 02:02
Hugo: Po alko matma nie idzie

23 kwi 02:02
kyrtap : i jeszcze m = −1/2
23 kwi 02:02
razor: | | 1 | |
a m = − |
| to gdzie uciekło? |
| | 2 | |
23 kwi 02:03
kyrtap : kurde zadania lepiej widzę mi idą po 2 w nocy niż ranem lub po południu
23 kwi 02:03
razor: no

23 kwi 02:03
kyrtap : dobra oki
23 kwi 02:03
23 kwi 02:04
kyrtap : Marcin śpisz?
23 kwi 02:04
Marcin: heeh

Napisz maturę w nocy

23 kwi 02:04
Marcin: Idę na kolację, chwilka

23 kwi 02:04
razor: odpisałem ci Hugo, jeśli o to ci chodziło
23 kwi 02:06
kyrtap : kolejne zadanie ?
23 kwi 02:07
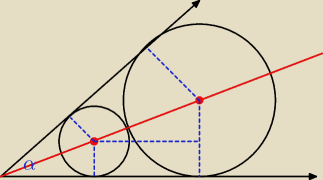
Marcin: W kąt o mierze 60 ∘ wpisano dwa okręgi styczne zewnętrznie. Promień mniejszego okręgu ma
długość 1. Oblicz długość promienia drugiego okręgu.
Za chwilkę wracam

23 kwi 02:07
kyrtap : też idę po jakiegoś chickena
23 kwi 02:07
asdf: polecam Wam:
http://www.collabedit.com
bedzie Wam wygodniej

tylko jak juz jeden jest trakcie pisania to niech reszta czeka

23 kwi 02:09
Hugo: dziękuje za pomoc, nie wiedziałem nawet szczerze
23 kwi 02:10
kyrtap : tu jest wygodniej bo Marcin wszystko rysuje
23 kwi 02:14
kyrtap : 
23 kwi 02:15
razor: Marcin r = 3?
23 kwi 02:19
23 kwi 02:20
Marcin:
23 kwi 02:21
Marcin: Razor w sumie nie wiem, jeszcze nie liczyłem. Chwilka

23 kwi 02:21
Marcin: A nie no jednak Hugo zepsułeś zabawę

23 kwi 02:22
kyrtap : ee nie chcem rozwiązania
23 kwi 02:24
razor:
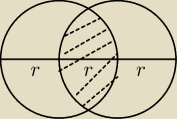
To teraz coś ode mnie

Oblicz pole zakreskowanej figury, przyjmując dane podane na rysunku
23 kwi 02:26
kyrtap : razor co to za zadanie dziwaczne

23 kwi 02:30
razor: wygrzebałem swój sprawdzian z pierwszej klasy skądś

takie zadanko tam było
23 kwi 02:32
Hugo: był na to wzór xd
23 kwi 02:33
Hugo: Panowie, jutro ma lać

⇔ siedzimy cały dzień nad matmą

23 kwi 02:34
Marcin: był na to wzór?
23 kwi 02:34
kyrtap : i polakiem

23 kwi 02:35
kyrtap : bezendu chyba już bawi się z nami co?
23 kwi 02:37
Hugo: tzn coś mi sie kojarzy gdzies dawno temu w necie znalazłem zależnosć

ale to takie gadanie
...
23 kwi 02:37
kyrtap : nie bawi *
23 kwi 02:37
Marcin: razor to zadanie ze szkoły średniej? wydaje się proste, a nigdy takiego nie widziałem i jakoś
mnie chyba zaćmiło.
23 kwi 02:39
kyrtap : tak samo i mnie

23 kwi 02:39
Hugo:
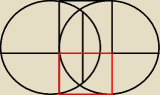

prastara wiedza powraca
23 kwi 02:40
razor: Marcin zadanko z pierwszej klasy liceum profil rozszerzony

23 kwi 02:42
Trivial: Do której siedzicie?

23 kwi 02:43
Hugo: kwadrat r
2
| | πr2 | |
Różnica: r2 − |
| = {4r 2−πr}{4} I to wszystko razy dwa  → {r(4r−π}{2} |
| | 4 | |
23 kwi 02:44
razor: wstaję jutro o 6 więc chyba nie kładę sie spać
23 kwi 02:44
Marcin: Hugo co Ty nam tutaj sugerujesz tym rysunkiem?

Że pole tego zaznaczonego obszaru, to będzie
kwadrat?

23 kwi 02:44
kyrtap : no nie wiem do której chcecie?
23 kwi 02:44
Hugo: | | 4r2−πr | | r(4r−π) | |
... |
| I to wszystko razy dwa → |
|  HUGO wygrał internet |
| | 4 | | 2 | |
23 kwi 02:45
Marcin: Trivial no ile się da

Nie myśl tylko że tak kujemy matmę ze strachu przed maturą

ja wolę
się po prostu uczyć w nocy

23 kwi 02:45
kyrtap : ja również Marcin byśmy się dogadali widzę na studiach jakbyśmy razem mieszkali xd
23 kwi 02:46
Marcin: Sugerujesz nocne picie?

23 kwi 02:47
Hugo:
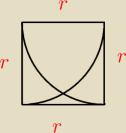
Dokładnie tak Marcinie, słabo rysuje

23 kwi 02:47
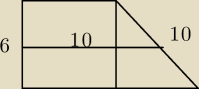
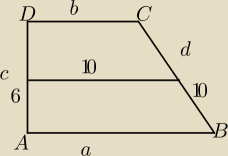
Marcin: Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość
10. Oblicz długości podstaw trapezu.
Teraz to

23 kwi 02:47
Marcin: No a na jakiej podstawie to stwierdzasz?

23 kwi 02:49
Hugo: Są studia
dzienne

wieczorowe

zaoczne

Wy stworzycie studia nocne

2:00−6:00
23 kwi 02:50
kyrtap : no raczej nie inaczej

23 kwi 02:51
razor: 6 i 14
23 kwi 02:51
Marcin: razor Ty też zdajesz maturę?

23 kwi 02:52
Hugo:
niezaproste to zadanko ;>
23 kwi 02:53
zombi: Podpowiedź do tego zadania, co rzuciłeś Marcin.
| | a+b | |
Odcinek łączący środki ramion ma długość |
| , gdzie a i b to podstawy trapezu. |
| | 2 | |
23 kwi 02:53
razor: tak, pierwszy raz
23 kwi 02:53
zombi: Nie odświeżyłem przez chwilkę, a tu bum rozwiązane

23 kwi 02:53
kyrtap :
23 kwi 02:54
razor: a co z moim zadankiem?

23 kwi 02:55
kyrtap : i potem tw. Pitagorasa
23 kwi 02:56
kyrtap : razor jakieś takie inne te twoje zadanie
23 kwi 02:56
Marcin: razor przecież Hugo coś tam napisał, dobrze miał?

23 kwi 02:57
razor: przez całe liceum takie miałem

jak chcecie jakieś dziwne nietypowe zadanie z któregoś działu
to mogę poszukać odpowiedniego sprawdzianu, o ile go jeszcze mam

23 kwi 02:57
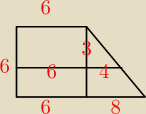
Hugo:
23 kwi 02:57
Hugo: Hugo 2:0

... a tak sie zniego wszyscy śmiali że debil.. biedny Hugo </3

23 kwi 02:58
kyrtap : Hugo

23 kwi 02:59
razor: Hugo ma źle

23 kwi 03:01
Marcin: No biedny, biedny

CKE daje zadania na podobnym poziomie

23 kwi 03:01
Marcin: Pokazać, że dla każdej liczby całkowitej n liczba n 5 − n jest podzielna przez 5.

23 kwi 03:03
Marcin: n
5−n ma być

23 kwi 03:03
Marcin: razor ja nie mam pomysłu, może ktoś inny. Pewnie rozwiązanie jest banalne

23 kwi 03:04
Hugo: robiłem to tydzień temu

23 kwi 03:04
Marcin: To przypomnij może innym jak to rozwiązać

23 kwi 03:07
razor:
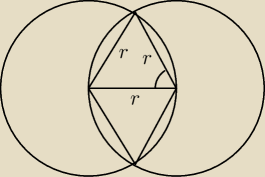
znamy pola tych trójkątów, zaznaczony kąt, teraz pozostaje obliczyć pole tego wycinka

pytanie jak to zrobić

23 kwi 03:11
razor: tych 4 wycinków* miało być
23 kwi 03:12
kyrtap : myślimy myślimy
23 kwi 03:15
23 kwi 03:16
razor: nikt nie pisze to ja napiszę

n
5 − n = n(n
4−1) = n(n
2−1)(n
2+1) = n(n−1)(n+1)(n
2−4+5) = (n−2)(n−1)n(n+1)(n+2) +
5n(n−1)(n+1)
Iloczyn pięciu kolejnych liczb całkowitych (wśród nich jest wielokrotność 5) + 5 razy jakaś
liczba całkowita = liczba podzielna przez 5
23 kwi 03:18
razor: Marcin dobrze
23 kwi 03:18
Hugo: Marcin:
n5−n = n(n4−1)= n(n2−1)(n2+1)=(n−1)n(n+1)(n2+1)
Mamy tu kolejne liczny całkowite 5 10 i jeżeli to nie jest zadna podzielna przez 5 to
(n−1)n(n+1)(n2+1)
n2 = 5k +2 v n2 = 5k +3
...
(5k +2)2 +1 |5 v (5k +3)2 +1 |5
23 kwi 03:18
ZKS:
Macie jak zrobicie do dam kolejne.
Wiadomo że wielomian W(x) = 3x3 − 5x + 1 ma trzy pierwiastki rzeczywiste x1, x2 oraz x3.
Bez wyznaczania tych pierwiastków obliczyć wartość wyrażenia (x1 + 1)(x2 + 1)(x3 + 1).
23 kwi 03:20
kyrtap : ja spadam miski do łózka bo jutro tez muszę wstać o 6
23 kwi 03:22
razor: ZKS wzory Viete'a?
23 kwi 03:23
Marcin: Cześć

23 kwi 03:23
Marcin: Też m się z wzorami Viete'a kojarzy. Tylko że wzory 3st. nie obowiązują na maturce

23 kwi 03:23
razor: ja np. ich nigdy nie pamiętam i zawsze muszę je wyprowadzać gdy zachodzi potrzeba

23 kwi 03:25
ZKS:
Tak. Pójdzie wzorami Viete'a.
23 kwi 03:25
Hugo: ZKS: my gimby nie wymagaj

//coś na fb pisali na ściąga.pl że jakąś nocke maturzysty w tym
matma R warto mysle ogarnąć, to jakoś na dniach....
Wymnożyłem sb (x1 + 1)(x2 + 1)(x3 + 1).ale jakoś tego nie czuje
23 kwi 03:27
23 kwi 03:33
Hugo: ja pauzuje z wielomianami z plani z .... Muszę dokończyć 3 zadanka z trygonometri ;x
23 kwi 03:34
Marcin: według mnie ok zrobione

tzn zamiana na wzory Viete'a

23 kwi 03:34
razor: dobra wyprowadziłem sobie

dla W(x) = 3x
3 − 5x + 1
x
1+x
2+x
3 = 0
| | 5 | |
x1x2 + x2x3 + x1x3 = − |
| |
| | 3 | |
(x
1+1)(x
2+1)(x
3+1) = x
1x
2x
3 + x
1x
2 + x
2x
3 + x
1x
3 + x
1+x
2+x
3 + 1 = 1 − 2 = −1
23 kwi 03:35
Marcin: 
23 kwi 03:36
razor: spóźniłem się

ale przynajmniej przypomniałem sobie wyprowadzanie wzorów Viete'a
23 kwi 03:37
Marcin: razor wyprowadzasz je tak?
a(x−x
1)(x−x
2)(x−x
3)=ax
3+bx
2+cx+d wymnażasz i masz?

23 kwi 03:39
razor: tak
23 kwi 03:39
ZKS:
To ja pokażę nieco prostszy sposób.
Mamy policzyć (x
1 + 1)(x
2 + 1)(x
3 + 1) więc jeżeli policzymy W(x − 1) to
dostaniemy pierwiastki o 1 większe.
W(x − 1) = 3(x − 1)
3 − 5(x − 1) + 1 = 3x
3 − 9x
2 + 4x + 3
23 kwi 03:39
Marcin: No na to na pewno bym nie wpadł

23 kwi 03:41
ZKS:
Kolejne.
Rozwiąż nierówność
(√x)log8(x) ≥ 3√16x.
23 kwi 03:41
Hugo: Nie wiem jak wy ale matma wciąga 8) lepsze niż alkohol motoryzacja czy kobiety
mam pytanko

mam równanie
sin
2x=2cosx
z jedynki tryg.
1−cos
2x−2cosx=0
t:=cox
1−t
2−2t=0
Δ=8
t
1 = −1+
√2 v t
2= 1+
√2
cox=−1+
√2 v cox=1+
√2
to jest dziwne czy złe ?
23 kwi 03:42
23 kwi 03:47
Hugo: ZKS: Mam wrażenie ze to mature R nie obejmuje

?
23 kwi 03:48
Marcin: No ja bym tego raczej nie rozwiązał..
23 kwi 03:49
ZKS:
Hugo odpowiedź

. Mam pytanie wolfram?

23 kwi 03:49
Hugo: co wolfram bo ja tępy w żartach

?
23 kwi 03:50
ZKS:
Jak rozwiązałeś samemu czy wrzuciłeś do wolframa? Bo zadanie strasznie szybko zrobiłeś.

23 kwi 03:51
Marcin: ZKS, wolfram też tego nie ogarnia

23 kwi 03:55
Hugo: Nie wrzuciłem do wolframu xd nie wiem co to jest(domyślam sie)... Jestem świeżo po logach i
miałem podobne zadanie

teraz lece w tryge a mam jeszcze braki w ciągach które są
stosunkowo łatwe ;3 i potem testy których jeszcze nie zacząłem


Idę spać bo w zbiorze zadań(A.Kiełbasa str.104) doszedłem do zadań trywialnych i wolę się nie
dołować... 'Jutro też jest dzień' .. Dobranoc wszystkim

!
23 kwi 03:55
Marcin: Cześć

23 kwi 03:56
ZKS:
Dobranoc.

23 kwi 04:01
razor: zrobiłem to ZKS i taki sam wynik jak u Hugo

Ale nie uniknąłem zajrzenia do notatek
23 kwi 04:02
ZKS:
To napisz żeby
Marcin zobaczył skąd taki wynik.

23 kwi 04:08
Marcin: No dokładnie

23 kwi 04:09
razor: niech Marcin sobie podstawi log
8x = a ⇒ x = 8
a = 2
3a i sam zrobi

trochę pisania jest
23 kwi 04:11
ZKS:
To ładną wskazówkę dostałeś więc teraz dokończ i napisz czy dostałeś ten sam wynik.
23 kwi 04:13
Marcin: ok, będę coś jutro myśleć może. Chociaż z drugiej strony, to materiał dopiero na studia

23 kwi 04:13
ZKS:
To kolejne.
Udowodnić nierówność dla dowolnych a , b oraz c
a4 + b4 + c4 ≥ abc(a + b + c).
23 kwi 04:16
razor: pewnie trzeba pobawić się nierównościami między średnimi, ale nie wiem za bardzo jak

a
jakieś zadania bardziej maturalne masz?
23 kwi 04:35
zombi: Albo tak, z ciągów jednomonotonicznych, załóżmy bez straty ogólności, że: a≥b≥c.
Zatem
[a
2 b
2 c
2] [a
2 b
2 c
2]
[b c a] ≤ [a b c]
[c a b] [a b c]
ckd.
Albo ze średnich jak mówi razor:
a
4 + b
4 + c
4 ≥ a
2b
2 + a
2c
2 + b
2c
2 =
| | a2b2 + a2c2 | | a2b2 + b2c2 | | a2c2 + b2c2 | |
= ( |
| ) + ( |
| ) + ( |
| ) ≥ |
| | 2 | | 2 | | 2 | |
a
2bc + b
2ac + c
2ab = abc(a+b+c)
ckd
23 kwi 07:28
5-latek:
Jak wroce z pracy to napiszse Wam rozwiazanie tego zadania z 01:05
A na rozrywke macie nastepne
Zadanie nr 1.
Niech h bedzie dlugoscia wysokosci trojkata prostokatnego opuszczonej z wierzcholka kąta
prostego. r− dlugoscia promienia okrego wpisanego wten trojkat
Udowodnic ze
Zadanie nr 2
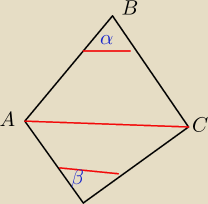
Czy istnieje czworokąt ABCD ktorego dlugosci bokow spelniaja uklad warunkow
{AB<CD<AD<BC
{AB+BC=CD+DA
{AB
2+BC
2=CD
2+DA
2 ?
Przeprowadzic dowod geometryczny i algebraiczny
23 kwi 08:53




 Rysunek będzie chyba mniej więcej jakiś taki
Rysunek będzie chyba mniej więcej jakiś taki 





 No to macie zadanko na noc pelna wrazen
No to macie zadanko na noc pelna wrazen  dany jest okrąg o(A,r) i punkt P .
Udowodnic ze dla kazdej prostej przechodzacej przez P i nierozlacznej z o(A,r) iloczyn
odleglosci punktu P od punktow przeciecia tej prostej z okregiem wynosi |Ap2−r2|
dany jest okrąg o(A,r) i punkt P .
Udowodnic ze dla kazdej prostej przechodzacej przez P i nierozlacznej z o(A,r) iloczyn
odleglosci punktu P od punktow przeciecia tej prostej z okregiem wynosi |Ap2−r2|
 Ale może browar
Ale może browar 


 Teraz jak już wiemy że są równe, to
|BD|=x
|DC|=2x
Teraz jak już wiemy że są równe, to
|BD|=x
|DC|=2x 











 napisałem również do Fringsa
napisałem również do Fringsa 

 Dobranoc maturzysci
Dobranoc maturzysci


 PX*PY=|AP2−r2|
Dalej nie macie pomysłów?
PX*PY=|AP2−r2|
Dalej nie macie pomysłów? 



 Tak?
Tak?
 A miało być troszkę inaczej
A miało być troszkę inaczej 




 Za chwilę coś innego będziemy robić. A to zadanie to
Twoja zasługa, brawo
Za chwilę coś innego będziemy robić. A to zadanie to
Twoja zasługa, brawo 









 Napisz maturę w nocy
Napisz maturę w nocy 


 tylko jak juz jeden jest trakcie pisania to niech reszta czeka
tylko jak juz jeden jest trakcie pisania to niech reszta czeka 




 To teraz coś ode mnie
To teraz coś ode mnie  Oblicz pole zakreskowanej figury, przyjmując dane podane na rysunku
Oblicz pole zakreskowanej figury, przyjmując dane podane na rysunku

 takie zadanko tam było
takie zadanko tam było
 ⇔ siedzimy cały dzień nad matmą
⇔ siedzimy cały dzień nad matmą 

 ale to takie gadanie
...
ale to takie gadanie
...


 prastara wiedza powraca
prastara wiedza powraca


 → {r(4r−π}{2}
→ {r(4r−π}{2} Że pole tego zaznaczonego obszaru, to będzie
kwadrat?
Że pole tego zaznaczonego obszaru, to będzie
kwadrat? 
 HUGO wygrał internet
HUGO wygrał internet Nie myśl tylko że tak kujemy matmę ze strachu przed maturą
Nie myśl tylko że tak kujemy matmę ze strachu przed maturą  ja wolę
się po prostu uczyć w nocy
ja wolę
się po prostu uczyć w nocy 

 Dokładnie tak Marcinie, słabo rysuje
Dokładnie tak Marcinie, słabo rysuje 


 wieczorowe
wieczorowe  zaoczne
zaoczne  Wy stworzycie studia nocne
Wy stworzycie studia nocne  2:00−6:00
2:00−6:00


 niezaproste to zadanko ;>
niezaproste to zadanko ;>




 jak chcecie jakieś dziwne nietypowe zadanie z któregoś działu
to mogę poszukać odpowiedniego sprawdzianu, o ile go jeszcze mam
jak chcecie jakieś dziwne nietypowe zadanie z któregoś działu
to mogę poszukać odpowiedniego sprawdzianu, o ile go jeszcze mam 

 ... a tak sie zniego wszyscy śmiali że debil.. biedny Hugo </3
... a tak sie zniego wszyscy śmiali że debil.. biedny Hugo </3 


 CKE daje zadania na podobnym poziomie
CKE daje zadania na podobnym poziomie 





 znamy pola tych trójkątów, zaznaczony kąt, teraz pozostaje obliczyć pole tego wycinka
znamy pola tych trójkątów, zaznaczony kąt, teraz pozostaje obliczyć pole tego wycinka  pytanie jak to zrobić
pytanie jak to zrobić 
 n5 − n = n(n4−1) = n(n2−1)(n2+1) = n(n−1)(n+1)(n2−4+5) = (n−2)(n−1)n(n+1)(n+2) +
5n(n−1)(n+1)
Iloczyn pięciu kolejnych liczb całkowitych (wśród nich jest wielokrotność 5) + 5 razy jakaś
liczba całkowita = liczba podzielna przez 5
n5 − n = n(n4−1) = n(n2−1)(n2+1) = n(n−1)(n+1)(n2−4+5) = (n−2)(n−1)n(n+1)(n+2) +
5n(n−1)(n+1)
Iloczyn pięciu kolejnych liczb całkowitych (wśród nich jest wielokrotność 5) + 5 razy jakaś
liczba całkowita = liczba podzielna przez 5



 //coś na fb pisali na ściąga.pl że jakąś nocke maturzysty w tym
matma R warto mysle ogarnąć, to jakoś na dniach....
Wymnożyłem sb (x1 + 1)(x2 + 1)(x3 + 1).ale jakoś tego nie czuje
//coś na fb pisali na ściąga.pl że jakąś nocke maturzysty w tym
matma R warto mysle ogarnąć, to jakoś na dniach....
Wymnożyłem sb (x1 + 1)(x2 + 1)(x3 + 1).ale jakoś tego nie czuje


 tzn zamiana na wzory Viete'a
tzn zamiana na wzory Viete'a 


 ale przynajmniej przypomniałem sobie wyprowadzanie wzorów Viete'a
ale przynajmniej przypomniałem sobie wyprowadzanie wzorów Viete'a


 mam równanie
sin2x=2cosx
z jedynki tryg.
1−cos2x−2cosx=0
t:=cox
1−t2−2t=0
Δ=8
t1 = −1+√2 v t2= 1+√2
cox=−1+√2 v cox=1+√2
to jest dziwne czy złe ?
mam równanie
sin2x=2cosx
z jedynki tryg.
1−cos2x−2cosx=0
t:=cox
1−t2−2t=0
Δ=8
t1 = −1+√2 v t2= 1+√2
cox=−1+√2 v cox=1+√2
to jest dziwne czy złe ?
 ?
?
 . Mam pytanie wolfram?
. Mam pytanie wolfram? 
 ?
?


 teraz lece w tryge a mam jeszcze braki w ciągach które są
stosunkowo łatwe ;3 i potem testy których jeszcze nie zacząłem
teraz lece w tryge a mam jeszcze braki w ciągach które są
stosunkowo łatwe ;3 i potem testy których jeszcze nie zacząłem 
 Idę spać bo w zbiorze zadań(A.Kiełbasa str.104) doszedłem do zadań trywialnych i wolę się nie
dołować... 'Jutro też jest dzień' .. Dobranoc wszystkim
Idę spać bo w zbiorze zadań(A.Kiełbasa str.104) doszedłem do zadań trywialnych i wolę się nie
dołować... 'Jutro też jest dzień' .. Dobranoc wszystkim  !
!


 Ale nie uniknąłem zajrzenia do notatek
Ale nie uniknąłem zajrzenia do notatek


 trochę pisania jest
trochę pisania jest

 a
jakieś zadania bardziej maturalne masz?
a
jakieś zadania bardziej maturalne masz?
 Jak wroce z pracy to napiszse Wam rozwiazanie tego zadania z 01:05
A na rozrywke macie nastepne
Zadanie nr 1.
Niech h bedzie dlugoscia wysokosci trojkata prostokatnego opuszczonej z wierzcholka kąta
prostego. r− dlugoscia promienia okrego wpisanego wten trojkat
Udowodnic ze
Jak wroce z pracy to napiszse Wam rozwiazanie tego zadania z 01:05
A na rozrywke macie nastepne
Zadanie nr 1.
Niech h bedzie dlugoscia wysokosci trojkata prostokatnego opuszczonej z wierzcholka kąta
prostego. r− dlugoscia promienia okrego wpisanego wten trojkat
Udowodnic ze