Dane sa punkty A( 2, -1) B= (3,0) Paulin: Dane sa punkty A=(2, −1) B=(3,0) a) wyznacz wzór funkcji b) wyznacz punkty przecięcia z osiami układu współrzędnych c) określ monotoniczność funkcji d) dla jakich argumentów f(x) <0 Jak to się rozwiązuje ?

Radek: Znasz wzór prostej kierunkowej ? y=ax+b a) −1=2a+b 0=3a+b Układ równań b)Miejsce zerowe, oraz miejsce przeciecia z osią OY współczynnik b. c) a>0 rosnaca, a<0 malejaca, a=0 stala d) Jak będziesz miała wzór to obliczysz

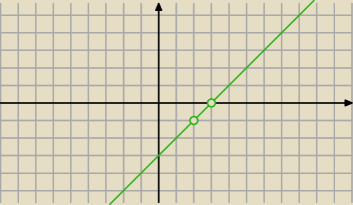
Ted: Te dwa punkty mogą leżeć na wykresach różnych funkcji. Wyznaczać mogą funkcję liniową

	0+1
y−0=		(x−3)
	3−2

y=x−3 Dalej sama −

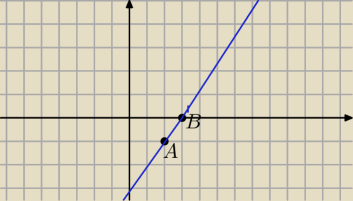
5-latek: napisz rownanie prostej przechodzacej przez dwa punkty i masz wzor funkcji Miejsca zerowe odczytaj z wykresu funkcji lub wstaw za y=0 do wzoru i wylicz x tak samo za x=0 podstaw do wzoru fubjcji i wylicz y Zobacz jaki wspolczynik stoi przy x i https://matematykaszkolna.pl/strona/41.html Rozwiaz ta nierownosc

Bogdan: Równanie prostej y = ax + b zadanej przez dwa punkty prościej wyznacza się bez układu równań.

	−1−0
W tym przypadku a =		= 1, y = (x − 2) − 1 ⇒ y = x − 3 albo od razu y = x − 3
	2−3

(korzystamy z zależności: y = a(x − x₀) + y₀, gdzie (x₀, y₀) to punkt należący do prostej).