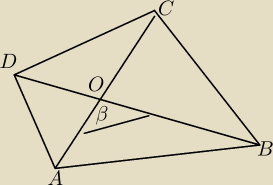
zadanka 5-latek: Marcin . najpierw spojrz tu https://matematykaszkolna.pl/forum/247271.html i pomoz koledze a potem takie zadanko z planimetrii Udowonij z e pole czworokata wypuklego rowne jest polowie iloczynu obu przekatnych i sinusa kata zawrtego miedzy nimi

Marcin: 5−latek dziękuję za zadanie

5-latek: Tylko je zrob

zombi: Przyjemne Takie luźne

Marcin:

	360−2β
Pole czworokąta to będą cztery trójkąty, kąty znam β, β,
	2

5-latek:

	360−2β
a		= 180−β
	2

Pole czworokata to pole 4 trojkatow tak jak napisales wiec czemu jest rownie pole trojkata AOB + pole trojkata BOC?

5-latek: Marcin czekam na obliczenia

Marcin: Chwilka 5−latek. U mnie są goście w domu, przecież mamy święta

5-latek: Podpowiem CI Przeciez znasz wzor na pole trojkata w zaleznosci od dlugosci bokow i kąta zawrtego miedzy nimi

5-latek: A. Nie zauwazylem twojego ostaniego postu . Wiec jak bedziesz juz mial czas to pisz

Marcin:

	1		1		1		1
PABCD=		AO*BO*sinβ +		OC*OD*sinβ +		OC*OB*sinβ +		OA*OD*sinβ =
	2		2		2		2

	AO*BO*sinβ		OC*ODsinβ		OC*OB*sinβ		OA*OD*sinβ
		+				+
	2		2		2		2

	AO*BO*sinβ+OC*ODsinβ+OC*OB*sinβ+OA*OD*sinβ		sinβ(OC*OD+OC*OB+OA*OD+AO*BO
=		=		=
	2		2

sinβ(OC*OD+OC*OB+OA*OD+AO*BO		1		1
	=		(sinβ([OC(OD+OB)+OA(OD+BO)]=
2		2		2

sinβ(OC+OA)(OD+OB)

Marcin: Oczywiście skorzystałem z tego, że sin(180−β)=sinβ

Piotr 10: Ile literek omg

Godzio: Jeśli mogę się czepić − powinniśmy zapisywać długość boku jako |AO| itd. a nie jako AO

5-latek: a OC+OA= ? i OD+OB=? i napisz koncowy wzor

Marcin: OC+OA= CA OD+OB= DB

sinβ(CA*DB)
2

Marcin: ok Godzio, zapamiętam

5-latek: czescx Godzio Maz calkowita racje . Nalezy sie tego uczyc od razu . Zreszta ja tez . Marcin popraw to w notatkach

Marcin:

5-latek: To nastepne . dane sa dlugosci bokow trojkata |AB|=10 |AC|= 6 i \BC|=14 Znajdz dlugosci odcinkow na jakie dwusieczna kąta przr wierzcholku C dzieli odcinek AB

Marcin: Za chwilkę. Lecę na dół do gości

Piotr 10: z nudów

x		6
	=		y=10−x
y		14

14x=60 − 6x 20x=60 x=3 y=7

5-latek: Ale niech tez Marcin sprobuje rozwiazac A dla Ciebie takie Wykaz ze dwusieczne katow trojkata przecinaja sie w jednyn punkcie Marcin niech tez sprobuje

Piotr 10: a długość dwusiecznej to ICDI² = 4*14 − 3*7=35 ICDI=√35

Piotr 10: Później idę ogladac film do prezentacji maturalnej ''Kanał'' A. Wajdy.

zombi: Jaki temat Piotr? bo tez mam ten film. Co do zadania to idzie z tw. Cevy, ale w formie trygonometrycznej.

Piotr 10: Powstanie warszawskie i sposób jego ujecia w literaturze, filmie i fotografi. Zaprezentuj temat na wybranych tekstach kultury. A Ty jaki?

5-latek: A jest to twierdzenie w liceum? Tu trzeba troche logiki wykazac

zombi: A mianowicie, jeśli

sinα1		sinβ1		sinγ1
	*		*		=1 To te czewiany przecinają się w jednym
sinα2		sinβ2		sinγ2

punkcie, a tak jest ponieważ α₁=α₂, β₁=β₂, γ₁=γ₂. ckd

zombi: Mam taki sam temat

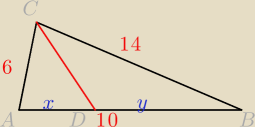
Marcin: x+y=10 x=10−y

10−y		y
	=
6		14

140−14y=6y 140=20y y=7 Rozwiązałbym tak samo

Piotr 10: Dobree heuehe ja mam 2 wiersze Baczyńskiego, Pamietnik z powstania warszawskiego i 2 filmy Kanał i Eroica

Marcin: Ja mam motyw snu w literaturze, ale dopiero na 29 maja.

Piotr 10: Ja mam napisana juz, bo mam 12 maja juz

zombi: Ja mam z literatury 2x Baczyński Pamiętnik Kolumbowie rocznik 20. i wiersz Anny Świrszczyńskiej Sztuka Kanał Wajdy Pianista film 2x plakaty muzyka Lao Che i 2 fotografie

Piotr 10: Z głowa na karabinie oraz Rodzicom ?

zombi: Z głową na karabinie i Pokolenie

Marcin: Nie przesadzacie czasem,? Strasznie dużo tego macie. Ja mam chyba 3 lektury i biblię

Piotr 10: no i mam z 5 fotografii, ale tutaj to bede wskazywal po prostu podczas omawiania prezentacji, np. 'Powstaniec wychodzacy z kanalu'' itd Mam prezentacje na 14 minut 57 sekund xD

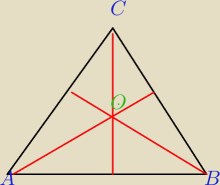
5-latek: To teraz pomysl nad tym drugim zadaniem o dwusiecznych

Marcin: Miałbym problem w tym dowodem

Marcin: Ja 'swojej pracy' jeszcze nawet nie czytałem

Piotr 10: Zapewne tutaj trzeba zauwazyc jesli punkt O nalezy do dwusiecznej kata ACB to , ze odleglosc punktu O od odcinka AC jest taka sama jak odleglosc punktu O od odcinka BC

Piotr 10: zombi a kiedy masz ustna z polaka ? tak bysmy sie wymienili pytaniami moze ?

zombi: Ja dopiero 26 maj

Piotr 10: eh ; / to najwyzej napisz na forum, to Ci podam swoje bo ja mam 12 maja

zombi: Ok, dzięki wielkie Ja chcę to tylko zdać, nie muszę mieć wielkiego wyniku.

5-latek: to napisze Mamy dowolny trojakt ABC Punkt O jest punktem przciecia sie dwusiecznej kąta A i dwusiecznej kątaB TEraz skoro O lezy na dwusiecznej kątaA to jest rownoodlegly od bokow AB i AC Teraz skoro lezy na dwusiecznej kąta B to jest rowmoodlegly od bokow Ab i BC A wiec jest tez rownoodlegly od bokow AC i BC , wiec lezy na dwusiecznej kąta C czyli jest punktem pezciecia sie wszystkich 3 dwusiecznych

Piotr 10: A myślisz, ze ja to co ? 6 punktów i dziekuje bardzo

zombi: http://pl.wikipedia.org/wiki/Twierdzenie_Cevy_%28trygonometryczne%29 może, ktoś sobie przyswoi Polski − byleby zdać.

5-latek: Nie rozumiem tego 6 punktow . Co to jest ?

Marcin: zombi jak tak patrzę na kawałek Twojej bibliografii, to jakoś nie mam wrażenia że chcesz 'tylko zdać' Ja chcę tylko zdać

zombi: Bo moja polonistka, kazała mi tyle nawrzucać

Marcin: 6 punktów − próg zdawalności matury ustnej

5-latek: Uczylem sie tego twierdzenia (dawno ) i sobie teraz przypomialem

Piotr 10: 5−latek na ustnej teraz jest tak. Max punktow to 20. a wiec zeby zdac trzeba miec 6 pkt. Ustnej nigdzie nie wliczaja na studia, dla mnie ogolem jest to bezsens, kazdy nauczyciel bedzie inaczej Ciebie pytal, a wiec tym samym jest to niesprawiedliwe. Ale cuz, takie zycie..

Marcin: Właśnie dlatego że do niczego nie potrzebujemy tej całej ustnej matury, tak łatwo jest ją zdać, (nie znam osoby która nie zdała)

Piotr 10: Za rok ma być tak, że uczniowie beda losowali tematy i maja 30 minut na przygotowanie sie do niego. Więc powracamy znow, tak jak kiedys bylo. Bardzo sie ciesze, ze mnie to ominielo

5-latek: Marcin . MOze wyda CI sie proste to zadanie ale masz Wierzcholki trojkata ABC leza na okregu . Znajdz srednice okregu gdy dane sa dlugosci boku |BC|=a oraz kaat lezacy naprzeciw tego boku (kąt BAC rowny alfa .

5-latek: Juz rozumiem . Jak ja pisalem to byla pisemnna z j. polskiego . Jak nie zaliczyl to byla ustna i losowal pytania

Marcin:

	a
d=		− twierdzenie sinusów. tak?
	sinα

5-latek: Tak ale do tego trzeba dojsc

Marcin: Mam to twierdzenie podane w tablicach, więc po co do tego dochodzić?

5-latek: Nie do twierdzenia tylko do wyniku . Pierwsze rysunek . I czemu twierdzisz ze Bok |CA| lezy na srednicy okregu ?

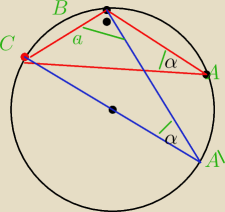
5-latek: masz rysunek do zadania

Marcin: Ja tak przecież nie twierdzę. Mam wzór:

	a
2R=		, który nie działa tylko w trójkącie prostokątnym..
	sinα

Utem: Działa.

Marcin: Utem: Twierdzenie sinusów działa tylko w trójkącie prostokątnym?

5-latek: MOje rozwiazanie do tego zadania jest takie |CA'|to srednica kątBAC =kątowi Ba'C =alfa bo sa oparte na tym samym luku jako kąty wpisane Wiemy ze kąt wpisany oparty na srednicy jest prosty wiec z trojakta A'BC mamy

	|BC|		a		a
sinalfa =		=		wiec 2R=		.
	|CA'|		2R		sinalfa

Ja tak to rozwiazalem . I masz nastepne zadanie Wykaz ze dlugosci a b c bokow trojkata promien R opisanego na num okregu oraz pole P trojkata sa zwiazane zaleznoscia

	a*b*c
P=
	4R

5-latek: Witaj Milu A jak bys Ty to rozwiazala (to z okregiem

Marcin: No ok, ale jak to by było na maturze? Musiałbym napisać tak jak Ty?

5-latek: Poczekajnmy na opinie Utem Na razie rob nastepne zadanie Przyda CI sie wzor z ostatniego zdania

Utem: Witajcie, trochę jestem rozleniwiona, z której godziny to zadanie.?

Marcin: Utem to Mila? Kolejny wzór, który jest w tablicach maturalnych

	a
2R=
	sinα

sinα * 2R= a

	1	a
sinα=
	2	2R

	1
P=		bc*sinα
	2

	1		a
P=		bc*
	2		2R

P=U{abc}{4R coś takiego?

5-latek: Z godziny 19:10

zawodus: 5− latek jak dla mnie to po prostu twierdzenie sinusów. Dowód, wg mnie powinien rozpatrywać trzy przypadki

Marcin:

	a
tam oczywiście ma być sinα=
	2R

vega: Nie "mieszać" maturzystom w głowach !

5-latek: Marcin tak ( do zadania wykaz ) I znowu moze babalne zadanie Udowodnij ze w trojkacie rownoraniennym srodkowe poprowadzone na ramiona sa rowne

Utem: wg mnie, sposób Marcina dobry. Nie zastanawiam się nad słusznością tw. sinusów, jest wykazane. Jeśli dostanę polecenie , to udowodnię, w tym zadaniu, po prostu z niego korzystam.

vega:

Utem:

a
	=2R
sinα

5-latek: Dobrze

5-latek: Pozdrawiam vega TYlko teraz tez sie usmiechnij niech wiem ze to Ty

vega:

5-latek:

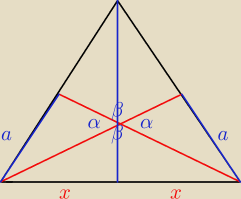
Marcin: To są przecież identyczne trójkąty. Mam to udowadniać?

5-latek: Tak udowodnic tak jak bys to tlumaczyl koledze z klasy ktory tego nie rozumie

Marcin: Te trójkąty mają jeden ten sam bok: 2x, ten sam kąt α i bok na przeciw jednego i drugiego jest równy a. Na tej podstawie mogę stwierdzić, że te trójkąty są takie same. Jak to zapisać 'matematycznie'?

5-latek: No na podstawie przystawania bok kąt bok. wydaje sie to takie oczywiste ale udowodnic trudniej Nie ? Na dzisiaj juz koniec . Znajde jakies ciekawe to wstawie Tobie OK?

Marcin: Dziękuję n−latku