Punkt A = (-2;4) jest jednym z wierzchołków trójkąta równoramiennego ABC, któreg
kamczatka: Punkt A = (−2;4) jest jednym z wierzchołków trójkąta równoramiennego ABC, którego pole jest
równe 20 i w którym |AC| = |BC|. Bok BC jest zawarty w prostej o równaniu y = x − 2. Oblicz
współrzędne wierzchołka C.
Tak się zastanawiam jak to wyliczyć ? Bo mogę wyliczyć prostą prostopadłą do prostej BC
przechodzącą przez punkt A, ale czy coś da ? Potem mogę punkty przecięcia się tych prostych i
to będzie środek odcinka BC. Ale nie wiem jak wierzchołek C wyliczyć.
20 kwi 15:27
kamczatka: pomoże ktoś ?
20 kwi 16:54
Marcin:
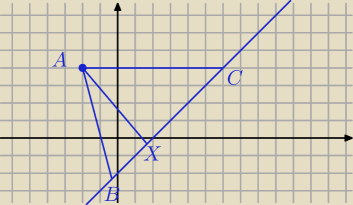
Wylicz sobie AX i podstaw do wzoru na pole trójkąta. Będziesz mieć wtedy długość BC.
20 kwi 17:11
zombi: A masz chociaż odpowiedzi, bo jeśli dobrze policzyłem to pokażę ci moje rozwiązanie.
20 kwi 17:12
Marcin: Później jak już masz BC i wiesz, że jest to równe AC, to Możesz policzyć ze wzoru na długość
odcinka, gdzie A znasz, a C=(x,x−2)
20 kwi 17:14
zombi: Ja już widzę dwie metody rozwiązania tego.
20 kwi 17:14
Marcin: Oczywiście powinny wyjść Ci dwa punkty C

20 kwi 17:16
zombi: Ma ktoś odpowiedź? Bo chciałbym sprawdzić czy moim sposobem wyjdzie.

20 kwi 17:16
Marcin: zombi a jak to liczysz?

20 kwi 17:18
zombi: Nie chce zapeszać, chciałbym sprawdzić z moją odpowiedzią, dopiero wtedy bym wrzucił.

Nie jest dużo szybciej, ale sposób trochę inny. Od tego.
20 kwi 17:20
Marcin: (−1;−3) i (5;3), tak masz?

20 kwi 17:32
zombi: Tak

Pierwszy sposób to taki sam jak twój Marcin.
Drugi sposób:
Wiemy, że C(x
c, x
c−2) oraz, że B(x
b, x
b−2)
Ponadto
|AC|=|BC|.
(x
c +2)
2 + (x
c−6)
2 = 2(x
c−x
b)
2
oraz
P=20
AC
→ = [x
c+2; x
c−6]
oraz
AB
→ = [x
b+2; x
b−6]
|x
c+2 x
c−6|
Zatem P=
12||
|x
b+2 x
b−6|
Tu miała być macierz 2x2, ale nie wiem, jak ją ładnie zapisać.
Czyli mamy dwa równania, dwie niewiadome i dość szybko wychodzi
x
c2−4x
c−5=0
20 kwi 17:40
Marcin: Nie przepadam za wektorami, dlatego zostaje przy swoim sposobie

20 kwi 17:54
kamczatka: ok dzięki jeszcze znalazłem sposób że potem wierzchołek C można obliczyć z równania okręgu.
Punkt A
robi za środek okręgu.
20 kwi 19:13
kamczatka: coś liczyłem ale nie wychodzi:
obliczyłem odległość punkty A do prostej y = x−2
wyszło że d = 4
| | 1 | |
potem z pola 20 = |
| a * 4 a = 10 |
| | 2 | |
i odległość punktu A od C
√(x + 2)2 + (x−2−4)2 = 10
x
2 − 4x − 30 = 0
Δ = 136 więc coś chyba nie tak po dziwne liczby wyjdą
21 kwi 11:16
5-latek: Ja tego nie liczylem ale naucz sie tez przyjmowac inne nieladne liczby
delta =136 jst tez pelnoprawna jak delta =144 (chocia z √144=12 =12 wyglada ladniej niz
√136
21 kwi 11:22
kamczatka: ale to wtedy wierzchołek C by miał współrzędne z pierwiastkiem a ma:
(−1;−3) i (5;3)
21 kwi 11:23
kamczatka: co robię nie tak ?
21 kwi 14:29
Marcin:
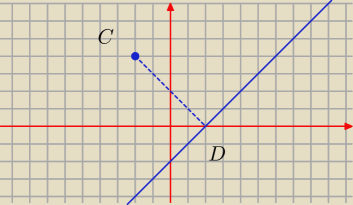
|CD| wyszło ci równe 4?
4
2+4
2=x
2
16+16=x
2
32=x
2
x=4
√2
21 kwi 14:36
kamczatka: chodzi Ci o odległość punktu A od prostej y = x −2 ?
21 kwi 14:46
kamczatka: aha juz wiem chodzi o wyliczenie połowy podstawy. Ale po co ją liczyć ? Bo ja robiłem tak że
obliczyłem odległość punktu A od prostej, potem wyliczyłem bok BC = 10 i na koniec ze wzoru na
długość odcinka AC i wychodzi równanie kwadratowe z Δ < 0
21 kwi 14:48
kamczatka:
wyznaczam odległość punktu A do prostej BC y = x −2
d = 4
wyliczam bok BC ze wzoru:
a = 10
|AC| = |BC| , C(x,x−2)
więc ze wzoru na długość odcinka AC:
√(x + 2)2 + (x − 2 − 4)2 = 10
x
2 − 4x − 30 = 0
21 kwi 14:54
Marcin: Pokaż jak liczysz odległość punktu od prostej

21 kwi 15:46
Beforeu: odleglosc punktu A od prostej y= x−2 i wychodzi ci h = 4 √2
21 kwi 15:56
Marcin: No tak, ale mi chodzi o to, żeby wiedział dlaczego

21 kwi 16:16
Beforeu: Jakie powinny być odpowiedzi? Wyszlo mi C (7 ,5 ) C(−3 ,−5 )
21 kwi 16:19
Marcin: (−1;−3) i (5;3), ja mam tak.
21 kwi 16:58
kamczatka: y − x − 2
A(−2;4)
| | |−2*−1+1*4 −2 | |
d= |
| |
| | √12+(−1)2 | |
teraz inny mi jeszcze wynik wyszedł bo wcześniej źle policzyłem mianownik
21 kwi 21:17
Marcin:
−x+y+2...
A(−2;4)
22 kwi 03:01
 Wylicz sobie AX i podstaw do wzoru na pole trójkąta. Będziesz mieć wtedy długość BC.
Wylicz sobie AX i podstaw do wzoru na pole trójkąta. Będziesz mieć wtedy długość BC.



 Nie jest dużo szybciej, ale sposób trochę inny. Od tego.
Nie jest dużo szybciej, ale sposób trochę inny. Od tego.

 Pierwszy sposób to taki sam jak twój Marcin.
Drugi sposób:
Wiemy, że C(xc, xc−2) oraz, że B(xb, xb−2)
Ponadto
|AC|=|BC|.
(xc +2)2 + (xc−6)2 = 2(xc−xb)2
oraz
P=20
AC→ = [xc+2; xc−6]
oraz
AB→ = [xb+2; xb−6]
|xc+2 xc−6|
Zatem P=12||
|xb+2 xb−6|
Tu miała być macierz 2x2, ale nie wiem, jak ją ładnie zapisać.
Czyli mamy dwa równania, dwie niewiadome i dość szybko wychodzi
xc2−4xc−5=0
Pierwszy sposób to taki sam jak twój Marcin.
Drugi sposób:
Wiemy, że C(xc, xc−2) oraz, że B(xb, xb−2)
Ponadto
|AC|=|BC|.
(xc +2)2 + (xc−6)2 = 2(xc−xb)2
oraz
P=20
AC→ = [xc+2; xc−6]
oraz
AB→ = [xb+2; xb−6]
|xc+2 xc−6|
Zatem P=12||
|xb+2 xb−6|
Tu miała być macierz 2x2, ale nie wiem, jak ją ładnie zapisać.
Czyli mamy dwa równania, dwie niewiadome i dość szybko wychodzi
xc2−4xc−5=0

 |CD| wyszło ci równe 4?
42+42=x2
16+16=x2
32=x2
x=4√2
|CD| wyszło ci równe 4?
42+42=x2
16+16=x2
32=x2
x=4√2
 wyznaczam odległość punktu A do prostej BC y = x −2
d = 4
wyliczam bok BC ze wzoru:
wyznaczam odległość punktu A do prostej BC y = x −2
d = 4
wyliczam bok BC ze wzoru:

