Schemat badania liczby rozwiązań Johnny Bravo: Zbadaj liczbę rozwiązań równania w zależności od parametru m x² + 2IxI = m² − 2 Mam problem z tego typu zadaniami, wgl nie znam schematu rozwiązywania ich. Jedynie umiem zrobić tak, że: przeżuciłem m² − 2 na lewą stronę, i rozważyłem 3 przypadki. 2 rozwiązania gdy delta > 0 1 gdy delta=0 brak gdy delta<0 Wyszły mi przedziały np. dla 0 rozwiązań (−1;1) ale mam dziwne wrażenie że to jest źle. Może ktoś to sprawdzić i ewentualnie wytłumaczyć mi łopatologicznie jak się rozwiązuje takie zadania?. Dziękuję z góry i pozdrawiam

Johnny Bravo: przerzuciłem* sorki

Tadeusz: x²+2|x|−m²+2=0 zauważ, że znak przy x nie ma wpływu na Δ Δ=(±2)²−4(−m²+2) Δ=4m²−4=4(m−1)(m+1) ...itd

Johnny Bravo: Czyli co dobrze jest to zrobione? Bo w tym temacie: https://matematykaszkolna.pl/forum/69263.html ktoś to zrobił inaczej, dlatego myślałem , że źle coś robię .

Saizou : można też tak x²+2lxl+1=m²−1 (lxl+1)²=m²−1 1 o kiedy m²−1<1 mamy 0 rozwiązań 2^o kiedy m²−1=1 mamy 1 rozwiązanie 3^o kiedy m−1<1 mamy 2 rozwiązania

Saizou : oczywiście chochlik 3^o kiedy m²−1>1

Johnny Bravo: No dobra , ale nadal nie wiem czy dobrze to zrobiłem czy źle?

Johnny Bravo: Tobie Saizou wyjdą przedziały z √2 a Tadeuszowi wyszłoby tak jak mi czyli z 1 i −1 przedziały. Ja już sam nie wiem jak ma być poprawnie

Tadeusz: niestety Johnny to my mamy źle. Tak można rozwiązywać równanie bez modułu.

Johnny Bravo: No ale w takim razie co jest złego w mojej metodzie, przecież dla zadań typu "Dla jakich parametrów m równanie ma 2 pierwiastki..." to jest dobra metoda, to dlaczego tutaj miałaby być zła? Nie potrafię tego zrozumieć.

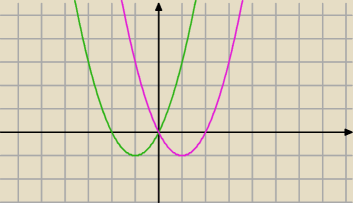
Tadeusz: na zielono y=x²+2x fiolet y=x²−2x

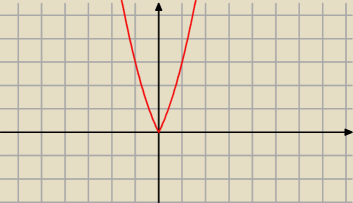
Tadeusz: a f(x)=x²+2|x|

Johnny Bravo: No dobra rozumiem, że ten wykres właściwy to jest część różowego po lewej i zielonego po prawej, które przecinają się w zerze, tak? No to jakbym zrobił tak że rozbijam na 2 przypadki x>0 i x<o to i tak to w rozwiązaniu nic nie zmieni bo jest b² licząc delte. Dlatego dalej nie kminie co jest złego w tej metodzie to mnie nurtuje

Johnny Bravo: o wyprzedziłeś

Tadeusz: rozumiesz różnicę?

Johnny Bravo: No właśnie nie , sęk w tym, że ciągle nie rozumiem, błędu w metodzie Δ> 0 ,Δ = 0, Δ<0 po rozbiciu wartości bezwzględnej na x>0 i x<0 czyli 2 przypadki. Co tutaj i tak nic nie zmienia bo jest b² licząc deltę. Na prawdę mam wielkie chęci żeby się tego nauczyć

Tadeusz: 1. Oni rozwiązywali to graficznie ... to najłatwiejsza metoda dla tego typu zadań

Tadeusz: Metoda algebraiczna ... z deltą nie jest błędem ... ale w takim zadaniu gdzie jest |x| sama delta nie wystarcza.

Johnny Bravo: w takim razie co jeszcze trzeba zrobić?

Tadeusz: Zauważ, że jeśli masz f(x)=x²+2x−m²+2 i analizujesz ilość miejsc zerowych to nie masz warunku czy mają być dodatnie, ujemne, tych samych czy różnych znaków ... interesuje Cię tylko ich ilość ... czyli badanie Δ Ale dla f(x)=x²+2|x|−m+2 sama Δ nie wystarcza. Rozpatrujesz przedziały x<0 i x>0 Zatem np dla x∊(−∞,0) jeśli dwa pierwiastki to oba ujemne zatem dodatkowo x₁+x₂<0 i x₁x₂>0

Johnny Bravo: Aaaa, to w taki sposób. Już rozumiem . A co do graficznej to można by było przenieść tą −2 na drugą stronę i mieć samo m² po prawej? wtedy wykres przesunęli byśmy o 2 jednostki w górę dla m²=2 mielibyśmy 1 rozwiązanie... itp?

Tadeusz: zauważ, że z warunku x₁x₂<0 −m²+2<0 (m−√2)(m+√2)>0 i to nakładasz na warunki z Δ I mamy to samo co z metody graficznej. ALE TAKIE ZADANIA NAJŁATWIEJ GRAFICZNIE

Tadeusz: DOKŁĄDNIE −

Johnny Bravo: Super, super, fajnie mi to wytłumaczyłeś, doceniam bardzo , szkoda że Ci piwka postawić nie mogę

Tadeusz: ...LICZY SIĘ DOBRE SŁOWO I CHĘCI −

Johnny Bravo: W takim razie myślę , że soczyste dziękuję Cie zadowoli

Tadeusz: −

Tadeusz: Pogodnych Świąt ... ja już zmykam w objęcia Morfeusza −