funkcja kwadratowa pk: Zbadaj liczbę rozwiązań równania w zależności od parametru m x² + 2IxI = m² − 2

M4ciek: 1^o Dla m < 0 i m > 0 x² + 2IxI = m² − 2 2^o Dla m = 0 x² + 2IxI = −2

pk: no tal ale po 1− co z x? po 2− m zawsze będzie w tej sytuacji dodatni

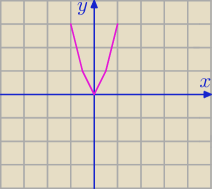
Godzio: f(x) = x² + 2|x| 0 rozwiązań dla m² − 2 < 0 ⇒ m ∊(−√2,√2) 1 rozwiązanie dla m² − 2 = 0 ⇒ m ∊{−√2,√2} 2rozwiązania dla m² − 2 > 0 ⇒ m ∊ (−∞,−√2)∪(√2,∞)

pk: nierozumiem. możęcie mi to wytłumaczyć?

Godzio: Na wstępie: 1 rozwiązanie to 1 punkt przecięcia się wykresu x² + 2|x| i m² − 2 wyobraź sobie że m² − 2 to proste poziome które przecinają wykres jeśli są one pod osią OX czyli m² − 2 < 0 −− czyli taka prosta nie przetnie nigdy wykres więc nie będzie rozwiązań jeśli jest m² − 2 > 0 to punkty przecięcia będą zawsze 2, lepiej to tak widać bo to bez różnicy czy potraktujesz jako prostą czy parabolę, ważne żeby dobrze to obliczyć

pk: to rozumiem, ale jak narysowałes ten wykres rozpatrzyles na x>0 i dla x< 0?

Godzio: Nie, tutaj nie trudno zauważyć że mamy symetrię częściową względem OY ⇒ f(|x|) ( (|x|)² = x²) Najpierw rysujesz wykres f(x) = x² + 2x Nakładając bezwzględność na x powodujesz że to co jest po lewej znika i to co jest po prawej odbija się na lewo, w ten sposób otrzymasz ten wykres

pk: dziękuje