Mila, potrzebuje cie! :) Albo ktoś inny mONdry Okła: Na każdym z sześciennych klocków, które ma Tomek, zapisana jest jedna cyfra. Pewnego dnia chłopiec ustawił w szereg siedem klocków, otrzymując liczbę siedmioicyfrową.Po chwili z utworzonego szeregu wysunął wszystkie klocki z cyfrą 5.Wówczas cyfry na pozostawionych klockach utworzyły liczbę 2010. Oblicz prawdopodobieństwo tego że otrzymana liczba siedmiocyfrowa była a) podzielna przez 5 i jak napisac do tego zbiór Ω? czy trzeba odrzucic 2 zera zeby nie były na początku ?

Okła: Godzio, help!

Marcin: Mogę Ci tak pomóc. https://matematykaszkolna.pl/forum/188526.html

Okła: Widziałem to, ale tam jest zapis ktory wlacza 0 na poczatku, a tego nie moze byc.

Marcin: Przykro mi, ale ja Ci nie pomogę Nie chce Tobie i sobie niepotrzebnie mieszać w głowie. Poczekajmy na kogoś ogarniającego prawdopodobieństwo

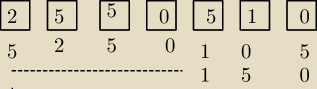
Mila: To zadanie logiczne. Na początku cyfra 2 albo 5, bo liczba siedmiocyfrowa. Dwójka występowała przed jedynką, bo nie przestawiał klocków, po niej gdzieś zero, potem gdzieś jedynka, po jedynce występowało znowu 0 jako ostatnia cyfra albo 5, a za nią zero. W każdym bądź razie na końcu albo 0 albo 5⇔liczba była podzielna przez 5 zawsze. P(A)=1

Okła: Jeju, dzieki. A juz myslalem ze tam jest jakis blad ! Nie zwrocilem uwagi na to ze te klocki ktore zostały były na tym samym miejscu.