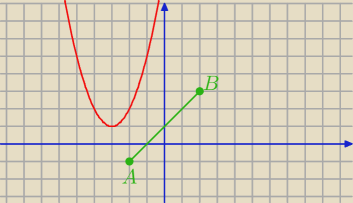
analityczna-pazdro Technik: Odcinek |AB| o koncach A=(−2,−1) i B=(2,3) jest podstawą trójkąta ABC. Wierzchołek C należy do prstej wykresu funkcji f(x)=x²+6x+10 Wyznacz C tak aby pole było najmniejsze? Co teraz robić ?

pigor: ... przeczytaj, czy dobrze przepisałeś..., jakiej prostej

pigor: ... moim zdaniem powinna to być prosta styczna i równoległa do odcinka AB

Technik: wierzchołek C należy do wykresu funkcji f(x)=x²+6x+10

Tadeusz: Na wykresie funkcji musisz odszukać punkt najbliżej położony od prostej przechodzącej przez A i B

Tadeusz: Na wykresie funkcji musisz odszukać punkt najbliżej położony od prostej przechodzącej przez A i B

Technik: Ale jak to zrobić ? Odległość punktu od prostej ?

Tadeusz: dokładnie

Technik: y=x²+6x+10 −x²−6x−10+y=0 x²+6x−y+10=0

|x2−6x+y+10|
√A2+B2

Co dać za A 1 czy 6 ?

pigor: ...

Tadeusz: ... przecież A, B i C to współczynniki w równaniu ogólnym prostej

Technik:

Technik: To jak to rozpisać ?

Technik: ok

	1
prosta ab:y=		x+2
	2

Tadeusz: ... zacznij od napisania równania prostej przez A i B

Tadeusz: ...sprawdź jeszcze raz

Technik: y=x+1

Tadeusz: −

Tadeusz: postać ogólna zatem to x−y+1=0 A=1 B=−1 C=1

pigor: ... , znajdź równanie prostej || do AB w postaci kierunkowej i rozwiąż układ równań tej prostej z równaniem paraboli tak, aby miał on dokładnie jedno rozwiązanie .

Tadeusz: ... teraz do wzoru na odległość punktu od prostej podstaw A, B i C oraz x_C i y_C

Technik: −x+y−1=0

|−x+y−1|
√2

A teraz co wstawić ?

Tadeusz:

	|xC−xC2−6xC−10+1|
d=
	√2

Mila: https://matematykaszkolna.pl/forum/150530.html

Technik: Dzięki Tadeusz

Technik: Mila skąd to x₀ czemu tak zapisujesz ?

Tadeusz: ... w Twojej treści jest "wyznacz C" ... czyli x_C i y_C

Tadeusz: bo tak jest we wzorze ogólnym ( punkt P o wsp. x_o, y_o)

Mila: Szukany punkt C=(x₀,y₀), C∊wykresu funkcji.

Technik: Czyli ten punkt ma wsp (x_c, x_c²+6x_c+10) A teraz co z tym zrobić ?

|−xc2−5xc−9|
	?
√2

Tadeusz: ... w linku masz wszystko wyjaśnione

Technik: Tylko, że wgl tego nie rozumiem. Inaczej bym wgl głowy tym nie zawracał...

Mila: Którego miejsca nie rozumiesz?

Technik: Co robimy teraz z tym co mam 19:12 ?

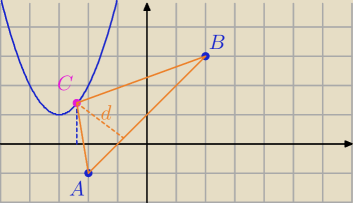
Mila: A=(−2,−1) i B=(2,3) Masz obliczone d

	|−xc2−5xc−9|
d=
	√2

mozesz to zapisać inaczej, z własności wart. bezwzględnej,

	|xc2+5xc+9|
d=
	√2

funkcja ( z licznika) y=x_c²+5x_c+9 przyjmuje tylko wartości dodatnie i parabola jest skierowana do góry (Δ=25−4*9<0, brak miejsc zerowych) Zatem ma wartość najmniejszą w wierzchołku paraboli,, będącej wykresem tej funkcji x_w=−2,5 y_w=f(−2,5)=(−2,5)²+6*(−2,5)+10=1,25 C=(−2,5;1,25)

	5   6,25+5*(− )+9   2
wtedy d=		jest najmniejsza
	√2

	2,75
d=		i to jest wysokość ΔABC (odległość punktu C od AB)
	√2

	1
PΔ=		*|AB|*d
	2

Technik: Ale czemu y=x²+5x+9 tam mam moduł ?

Mila: Przecież Ci napisałam x²+5x+9>0 dla x∊R to można moduł opuścic.

Technik: OK, teraz już zrozumiałe. Dziękuję !

Mila: To miło

Technik: Jeszcze muszę pomęczyć te diagramy venna nierówności i trochę analitycznej i 90%+ powinno być.