pom
Radek:
Jak wyznaczyć zbiór wartości
?
16 kwi 21:56
Hajtowy: Zw = <1;+oo) ?
16 kwi 21:57
Radek:
Nie chcę żadnych strzałów ani gotowców. Proszę o wskazówkę
16 kwi 21:59
52: na przedziały
1. x<0 2. x≥0
16 kwi 22:00
bezendu:
Hajtowy co Ty bredzisz
Na pewno masz źle bo to nie będzie taki zbiór.
16 kwi 22:01
5-latek: na poczatek przeksztalc to wyrazenie do postaci kanonicznej
16 kwi 22:02
ICSP: | 2|x| − 1 | | −3 | |
| = 2 + |
| . |
| |x| + 1 | | |x| + 1 | |
Teraz zastanów się jakie wartości może przyjąć mianownik.
16 kwi 22:02
Saizou :
| | 2lxl+2−3 | | 2(lxl+1)−3 | | 3 | |
f(x)= |
| = |
| =2− |
| |
| | lxl+1 | | lxl+1 | | lxl+1 | |
i dalej....
16 kwi 22:02
16 kwi 22:06
Radek: ?
16 kwi 22:18
zawodus: można, ale czy będzie prościej? nie bardzo
16 kwi 22:18
Mila:
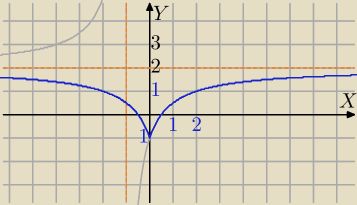
Rozważasz funkcję homograficzną:
| | 2x−1 | | 2(x+1)−2−1 | |
f(x)= |
| = |
| |
| | x+1 | | x+1 | |
y=2 asymptota pozioma
x=−1 asymptota pionowa.
Rysujesz wykres funkcji i odbijasz względem OY, część wykresu dla x≥0 (z prawej)
16 kwi 22:56
Radek:
A zbiór wartości odczytuję tak ?
Ale ja mam i w liczniku moduł i w mianowniku ?
16 kwi 23:07
Radek: ?
16 kwi 23:20
Mila:
Własnie dlatego Radku, tak możemy z wykresem postąpić.
Masz f(x) a potem rysujesz f(|x|) przez odbicie wzgledem OY
Zw=<−1,2) (niebieski wykres)
16 kwi 23:26
Radek:
A tak nie robi się jeżeli mam tylko w liczniku lub mianowniku ?
16 kwi 23:27
Radek: ?
17 kwi 00:01
marek: zbiór wartości czyli mianownik w tym przypadku różny od zera :
|x|+1≠0
|x|≠−1
x≠−1 v x≠1
ZW x∊R \ {−1; 1}
17 kwi 00:03
Radek:
Marek źle rozwiązanie jest Takie jakie podała Pani Mila
17 kwi 00:14
Radek: ?
17 kwi 20:26
Mila:
Czego nie rozumiesz, podaj treść i godzinę zapisu.
Umiesz rysować f(|x|)?
17 kwi 20:27
Radek:
Ale to się nie odbija jak mam tylko w liczniku i mianowniku moduł ?
17 kwi 20:40
pigor: ..., lub mój ...
gotowiec do szuflady,a może i dla
zainteresowanych :
| | 2|x|−1 | |
f(x)= |
| = w i x∊R ⇒ 2|x|−1= w(|x|+1) ⇔ |
| | |x|+1 | |
| | w+1 | |
⇔ (2−w)|x|= w+1 ⇔ 2−w≠ 0 i |x|= |
| ≥0 ⇔ |
| | 2−w | |
⇔ w≠2 i (w−2)(w+1)≤ 0 ⇔ −1≤ w <2 ⇔
w∊<−1;2) . ...
17 kwi 20:56
Mila:
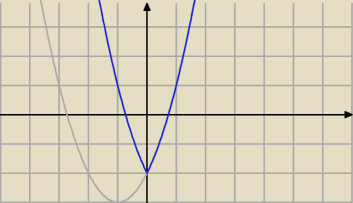
Radek , zobacz algebraiczny sposób
Pigora.
Myślałam, że łatwiejszy będzie geometryczny, ale masz kłopoty z wykresami.
Wyjaśniam wykresy.
Przyklad :
y=x2+2x−2→Symetria względem OY wykresu z prawej strony osi OY, reszte pomijasz i
otrzymujesz wykres →
y=|x|2+2|x|−2 czyli wykres y=x
2+2|x|−2
17 kwi 21:11
Radek:
Wolę rysunki ale nie odpowiedziała Pani na moje pytanie ?
20:40 ?
17 kwi 21:13
Mila:
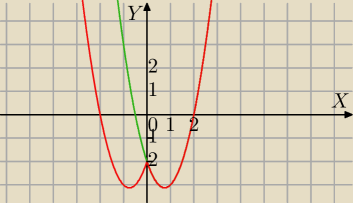y=2x2−3x−2
y=2|x|2−3|x|−2
17 kwi 21:16
Radek:
no tak takie rozumiem ale jak mam ułamkowe to gorzej
17 kwi 21:18
Mila:
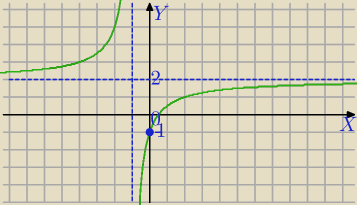
Właśnie Ci odpowiadam, dając inne przykłady.W Twoim zadaniu tam masz niewiadomą w wartości
bezwzględnej i w liczniku i w mianowniku, dlatego taki wykres narysoawałam o godzinie 22:56.
| | 2x−1 | |
g(x)= |
| tylko ten narysuję a w drugim wątku f(x) |
| | x+1 | |
Odbijemy tylko tę część wykresu dla x≥0
17 kwi 21:22
Mila:
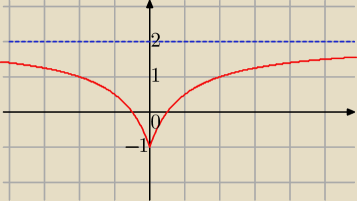
Z
w=<−1,2)
17 kwi 21:25
Radek:
Chyba coś zrozumiałem.
17 kwi 21:39
pigor: ... szkoda, że nie padły tu słowa : "funkcja f jest parzysta" ,
(dlaczego
), a wtedy coś ważnego o wykresie takiej funkcji . ...
17 kwi 23:14