planimetria
bezendu:

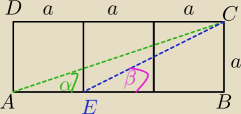
Na rysunku przedstawiono prostokąt złożony z 3 przystających kwadratów. Uzasadnij, że α+β=45
0
Próbowałem to rozpisywać ale β wychodzi 180
16 kwi 19:13
16 kwi 19:15
bezendu:
czemu tg ?
16 kwi 19:16
razor: Bo tak najłatwiej policzyć

gdybyś chciał stosować sinus albo cosinus musiałbyś liczyć
długość przeciwprostokątnych, wprowadzać oznaczenia itd. Tak jest szybciej
16 kwi 19:17
Mila:
α, β− katy ostre.
Ja liczyłabym sin α, cos α, sinβ, cosβ
sin(α+β)=sin α* cos β+ sinβ*cosα= ten wzór pamiętam
| | 1 | | 2 | | 1 | | 3 | |
= |
| * |
| + |
| * |
| = |
| | √10 | | √5 | | √5 | | √10 | |
| | 2 | | 3 | | 5 | | √2 | |
= |
| + |
| = |
| = |
| ⇔ |
| | √50 | | √50 | | 5√2 | | 2 | |
α+β=45
o
16 kwi 19:32
Draghan: Milu, czy to nie Ty pisałaś (do
bezendu nawet chyba), że "sposób rozwiązania
dopasowujemy do zadania"?

Mamy dane wprost wszystkie dane do obliczenia tangensów

Dlaczego z sinusów?

16 kwi 19:39
bezendu:
Ja to robiłem na dwa trójkąty pierwszy
β+90−β+90=180 i wychodziło masło maślane
16 kwi 19:51
Saizou : Mila napisała że wzór na sin(α+β) pamięta, bo jej się nie chce wyprowadzać wzoru na
tg(α+β), ani zaglądać do tablic xd
16 kwi 19:52
Draghan: Aaaaaa... No, chyba że jest tak, jak mówi
Saizou  bezendu
bezendu, dlaczego tak? Skąd wyprowadziłeś to równanie?

16 kwi 19:54
bezendu:
z tego drugiego trójkąta..
16 kwi 19:58
Draghan: To coś nie pykło. Ale to nic, masz poprawne rozwiązanie, teraz wnioskuj i zapamiętuj

16 kwi 20:07
bezendu:
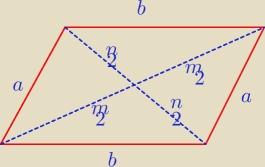
Przekątne równoległoboku o bokach a i b mają długościach przekątnych m i n. Uzasadnij, że
| | n2 | | n2 | | m2 | | m2 | |
a2+b2= |
| + |
| + |
| + |
| |
| | 4 | | 4 | | 4 | | 4 | |
Pierwszego nadal nie rozumiem

16 kwi 20:12
Mila:
Dokładnie tak, jak napisał Saizou.
Draghan,Razor, napisz do końca Twoje rozwiązanie. Jest ciekawe. Na pewno przyda się
komuś.
16 kwi 20:17
bezendu:
I tak tego nie rozumiem. A zadanie numer 2 ok ?
16 kwi 20:18
Saizou : bezendu a czy przekątne w równoległoboku przecinają się pod kątem prostym ?
16 kwi 20:19
bezendu:
Nie.
16 kwi 20:20
Saizou : wiec myśl dalej bo tak to nie jest dobrze xd
16 kwi 20:21
zawodus: Ja kiedyś to robiłem na zespolonych

Piękne zadanie

16 kwi 20:22
zawodus: Chodzi o pierwsze

16 kwi 20:23
bezendu:
już wiem
m
2=a
2+b
2−2ab*cosα
n
2=a
2+b
2−2abcos(180−α)
m
2+n
2=2(a
2+b
2)
Dostałem olśnienia
16 kwi 20:23
Mila:
Bezendu , napisać z oznaczeniami zadanie1)?
Zadanie z 20:12 żle
Przekątne nie są prostopadłe.
Komentarz: przekątne dzielą się na połowy,
Kąty przeciwległe równe,
Kąty sąsiednie dają w sumie 180o.
Niewielka poprawka musi byc.
16 kwi 20:23
Draghan: Kiedy pisałem, to się pojawiło kilka nowych wiadomości, ale szkoda mi wyrzucać moją pisaninę

Także wrzucam, co napisałem
 Bezendu
Bezendu, widzę że wyszedłeś z założenia, że przekątne przecinają się pod kątem prostym...
A tak nie jest

Kąt prosty między przekątnymi jest w równoległoboku o równych bokach, czyli
w rombie

A pierwsze? Najfajniejszy sposób (wg mnie) podał
razor. Masz obliczyć kąt α+β.
Masz tam też 2 trójkąty prostokątne, o znanych przyprostokątnych.
Czyli jeden trójkąt:
− ma kąt α i kąt prosty
− jego przyprostokątne mają długości 3 i 1.
Drugi trójkąt:
− ka kąt β i kąt proty
− jego przyprostokątne mają długości 2 i 1.
Mając przyprostokątne, łatwo policzyć tg, zarówno z α, jak i z β.
Masz dwa wyjścia: liczysz tgα i tgβ i sprawdzasz w tablicach, dla jakich kątów, po czym
dodajesz, albo liczysz tg(α+β) (bo tgα i tgβ znasz) i na podstawie tego odczytujesz z tablic
bezpośrednio kąt α+β

16 kwi 20:25
Saizou :
Draghan będziesz kozak jeśli podasz dokładne wartości tych kątów

16 kwi 20:28
bezendu:
Już drugie poprawiłem.
Poproszę to pierwsze z oznaczeniami.
16 kwi 20:30
Mila:
Piszę.
16 kwi 20:30
Draghan: Nie podam

Bo nie liczyłem tego

A teraz rozpościera się przede mną układ współrzędnych,
więc mam co robić

Głowię się nad analityczną, której nie lubię

Ale muszę zrobić to
zadanie, chociaż nie wiem, jak się za nie zabrać

16 kwi 20:31
bezendu:
Analityczna to jest piękna sprawa (oprócz wektorów)

16 kwi 20:36
Draghan: O, kolego! Wektory to jest piękna sprawa

Właśnie. Miałem się o tym pouczyć. Widziałem gdzieś na stronie wpis
Gustlika, dotyczący
liczenia pól figur z wektorów... Warto to znać

Ale najpierw trzeba znaleźć

Osobiście wolę geometrię na płaszczyźnie, taką zwykłą

16 kwi 20:40
bezendu:
To widzisz kolego, bo ja wolę wszystko oprócz geometrii na płaszczyźnie

16 kwi 20:41
zawodus: Wektory potrafią rozwalić każde zadanie praktycznie

16 kwi 20:41
Draghan: Teraz − jak mniemam − nastąpić musi dyskusja, na temat: "co znaczy 'rozwalić'?"

16 kwi 20:42
zawodus: Na to czekałem

16 kwi 20:43
Draghan: Doprecyzuj swoją wypowiedź z 20.41,
zawodusie 
16 kwi 20:45
bezendu:
rozwalić=rozwiązać=dojść do rozwiązania=mieć pomysł na rozwiązanie
16 kwi 20:45
zawodus: rozwalić=zburzyć=zniszczyć

16 kwi 20:46
Draghan: Drugi pierwiastek z rozwalić x
2=zepsuć

16 kwi 20:47
Draghan: O, właśnie

16 kwi 20:47
Mila:
I sposób:
W ΔABC:
|AC|
2=(3a)
2+a
2 z tw. Pitagorasa
|AC|=
√10a2=a
√10
| | |BC| | | a | | 1 | |
sinα= |
| = |
| = |
| |
| | |AC| | | a√10 | | √10 | |
| | |AB| | | 3a | | 3 | |
cosα= |
| = |
| = |
| |
| | |AC| | | a√10 | | √10 | |
W ΔEBC:
|EC|
2=(2a)
2+a
2=5a
2
|EC|=a
√5
| | EB | | 2a | | 2 | |
cosβ= |
| = |
| = |
| |
| | EC | | a√5 | | √5 | |
sin(α+β)=sin α* cos β+ sinβ*cosα=
| | 1 | | 2 | | 1 | | 3 | |
= |
| * |
| + |
| * |
| = |
| | √10 | | √5 | | √5 | | √10 | |
| | 2 | | 3 | | 5 | | √2 | |
= |
| + |
| = |
| = |
| ⇔ |
| | √50 | | √50 | | √50 | | 2 | |
α+β=45
II sposób
| | tgα+tgβ | |
tg(α+β)= |
| = |
| | 1−tgα*tgβ | |
α+β=45
o
16 kwi 20:48
bezendu:
Dziękuję, a czemu nie można ułożyć jakoś równań tak jak ja próbowałem ?
16 kwi 20:51
5-latek: No to lap dwa wzorki z geometrii analitycznej(zobacz czy sa w tablicach maturalnych
Dwusieczne kątow miedzy prostymi Ax+By+c=0 i A'x+B'y+C'=0
| Ax+By+C | | A'x+B'y+C' | |
| =+/− |
| |
| √A2+B2 | | √A'2+B'2 | |
Drugi
Styczna do okregu (x−p)
2+(y−q)
2=r
2 w punkcie A(x
1 y
1) gdzie (p,q) to wspolrzedne srodka
okregu
(x1−p)(x−p)+(y1−q)(y−q)=r2
16 kwi 20:57
zawodus: Żadnych z powyższych nie ma

16 kwi 21:12
zawodus: *Żadnego

16 kwi 21:12
16 kwi 21:14
Draghan: Kurczę

Znowu w sumie podpięte do cudzego tematu.
5−latek podał już trochę tych
ciekawych wzorów... Tylko gdzie one wszystkie są?

Trzeba to zebrać w jeden temat. Jutro

A co do wektorów, to znalazłem to, o czym mówiłem, że to widziałem:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3423
I jak sądzisz,
bezendu, wektory są takie złe?

16 kwi 21:25
bezendu:
Czytałem to zanim Ty byłeś na forum. I uwierz, że te wszystkie zadanie można zrobić bez pomocy
wektorów. Geometria analityczna to kilka rozwiązań a ja dostosowuje sobie najlepsze bez
wektorów.
16 kwi 21:26
Draghan: Nie wiesz, od kiedy ja jestem na forum

Skoro tak twierdzisz...

Przecież nie każę Ci tym liczyć.
16 kwi 21:28
bezendu:
Przypuszczam, że od niedawna ?

16 kwi 21:29
Draghan: A to dobrze przypuszczasz

16 kwi 21:32
Mila:
Bezendu, jakie równania układałeś, nie widzę.
16 kwi 21:34
bezendu:
β+90−β+90=180 i potem chciałem coś z α ułożyć ale już z pierwszego nic nie wyszło.
16 kwi 21:35
Mila:
Musiałbyć podać inną informację o drugim kącie w Δ prostokątnym.
16 kwi 21:49
bezendu:
Czyli jedyny sposób to tg ?
16 kwi 21:50
Mila:
Przecież podałam Ci dwa sposoby. Chyba zmęczony jesteś.
Na pewno jest inny jeszcze sposób.
16 kwi 22:22
bezendu:
Od 6 rano robię arkusze.. Czas odpocząć. Dziękuję.
16 kwi 22:24
Mila:
Dobranoc, kolorowych snów, bynajmniej nie o matematyce.

16 kwi 22:25
16 kwi 22:26
bezendu:
Jeszcze porobię trochę zadań z planimetrii.

16 kwi 22:30
zawodus: Bezendu chcesz prosty sposób?

16 kwi 22:40
bezendu:
Za zespolone dziękuję !

16 kwi 22:42
zawodus: Ale ten sposób to dwie linijki

16 kwi 22:47
Hugo: zawodus ja sie chetnie naucze

16 kwi 22:47
bezendu:
Ja już wiem, jak Ty możesz sposób wymyślić. Hugo ciekawe skąd znasz zespolone ?
16 kwi 22:49
zawodus:
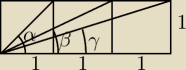
np takie zadanie

Wykaż, że α+β+γ=90

16 kwi 22:49
zawodus: to są oczywiście kwadraty

16 kwi 22:50
Hugo: ja nie znam ja sie chce nauczyć wszystkiego !

16 kwi 22:50
bezendu:
Zawodus jutro bo dziś już nie funkcjonuję. Dobranoc.
16 kwi 23:02
zawodus: To jutro

16 kwi 23:04
16 kwi 23:05
 Na rysunku przedstawiono prostokąt złożony z 3 przystających kwadratów. Uzasadnij, że α+β=450
Próbowałem to rozpisywać ale β wychodzi 180
Na rysunku przedstawiono prostokąt złożony z 3 przystających kwadratów. Uzasadnij, że α+β=450
Próbowałem to rozpisywać ale β wychodzi 180
 gdybyś chciał stosować sinus albo cosinus musiałbyś liczyć
długość przeciwprostokątnych, wprowadzać oznaczenia itd. Tak jest szybciej
gdybyś chciał stosować sinus albo cosinus musiałbyś liczyć
długość przeciwprostokątnych, wprowadzać oznaczenia itd. Tak jest szybciej
 Mamy dane wprost wszystkie dane do obliczenia tangensów
Mamy dane wprost wszystkie dane do obliczenia tangensów  Dlaczego z sinusów?
Dlaczego z sinusów? 
 bezendu, dlaczego tak? Skąd wyprowadziłeś to równanie?
bezendu, dlaczego tak? Skąd wyprowadziłeś to równanie? 

 Przekątne równoległoboku o bokach a i b mają długościach przekątnych m i n. Uzasadnij, że
Przekątne równoległoboku o bokach a i b mają długościach przekątnych m i n. Uzasadnij, że

 Piękne zadanie
Piękne zadanie 

 Także wrzucam, co napisałem
Także wrzucam, co napisałem  Bezendu, widzę że wyszedłeś z założenia, że przekątne przecinają się pod kątem prostym...
A tak nie jest
Bezendu, widzę że wyszedłeś z założenia, że przekątne przecinają się pod kątem prostym...
A tak nie jest  Kąt prosty między przekątnymi jest w równoległoboku o równych bokach, czyli
w rombie
Kąt prosty między przekątnymi jest w równoległoboku o równych bokach, czyli
w rombie  A pierwsze? Najfajniejszy sposób (wg mnie) podał razor. Masz obliczyć kąt α+β.
Masz tam też 2 trójkąty prostokątne, o znanych przyprostokątnych.
Czyli jeden trójkąt:
− ma kąt α i kąt prosty
− jego przyprostokątne mają długości 3 i 1.
Drugi trójkąt:
− ka kąt β i kąt proty
− jego przyprostokątne mają długości 2 i 1.
Mając przyprostokątne, łatwo policzyć tg, zarówno z α, jak i z β.
Masz dwa wyjścia: liczysz tgα i tgβ i sprawdzasz w tablicach, dla jakich kątów, po czym
dodajesz, albo liczysz tg(α+β) (bo tgα i tgβ znasz) i na podstawie tego odczytujesz z tablic
bezpośrednio kąt α+β
A pierwsze? Najfajniejszy sposób (wg mnie) podał razor. Masz obliczyć kąt α+β.
Masz tam też 2 trójkąty prostokątne, o znanych przyprostokątnych.
Czyli jeden trójkąt:
− ma kąt α i kąt prosty
− jego przyprostokątne mają długości 3 i 1.
Drugi trójkąt:
− ka kąt β i kąt proty
− jego przyprostokątne mają długości 2 i 1.
Mając przyprostokątne, łatwo policzyć tg, zarówno z α, jak i z β.
Masz dwa wyjścia: liczysz tgα i tgβ i sprawdzasz w tablicach, dla jakich kątów, po czym
dodajesz, albo liczysz tg(α+β) (bo tgα i tgβ znasz) i na podstawie tego odczytujesz z tablic
bezpośrednio kąt α+β 

 Bo nie liczyłem tego
Bo nie liczyłem tego  A teraz rozpościera się przede mną układ współrzędnych,
więc mam co robić
A teraz rozpościera się przede mną układ współrzędnych,
więc mam co robić  Głowię się nad analityczną, której nie lubię
Głowię się nad analityczną, której nie lubię  Ale muszę zrobić to
zadanie, chociaż nie wiem, jak się za nie zabrać
Ale muszę zrobić to
zadanie, chociaż nie wiem, jak się za nie zabrać 

 Właśnie. Miałem się o tym pouczyć. Widziałem gdzieś na stronie wpis Gustlika, dotyczący
liczenia pól figur z wektorów... Warto to znać
Właśnie. Miałem się o tym pouczyć. Widziałem gdzieś na stronie wpis Gustlika, dotyczący
liczenia pól figur z wektorów... Warto to znać  Ale najpierw trzeba znaleźć
Ale najpierw trzeba znaleźć  Osobiście wolę geometrię na płaszczyźnie, taką zwykłą
Osobiście wolę geometrię na płaszczyźnie, taką zwykłą 








 I sposób:
W ΔABC:
|AC|2=(3a)2+a2 z tw. Pitagorasa
|AC|=√10a2=a√10
I sposób:
W ΔABC:
|AC|2=(3a)2+a2 z tw. Pitagorasa
|AC|=√10a2=a√10













 Znowu w sumie podpięte do cudzego tematu. 5−latek podał już trochę tych
ciekawych wzorów... Tylko gdzie one wszystkie są?
Znowu w sumie podpięte do cudzego tematu. 5−latek podał już trochę tych
ciekawych wzorów... Tylko gdzie one wszystkie są?  Trzeba to zebrać w jeden temat. Jutro
Trzeba to zebrać w jeden temat. Jutro  A co do wektorów, to znalazłem to, o czym mówiłem, że to widziałem:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3423
I jak sądzisz, bezendu, wektory są takie złe?
A co do wektorów, to znalazłem to, o czym mówiłem, że to widziałem:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3423
I jak sądzisz, bezendu, wektory są takie złe? 
 Skoro tak twierdzisz...
Skoro tak twierdzisz...  Przecież nie każę Ci tym liczyć.
Przecież nie każę Ci tym liczyć.



 https://matematykaszkolna.pl/forum/246976.html
https://matematykaszkolna.pl/forum/246976.html





 np takie zadanie
np takie zadanie  Wykaż, że α+β+γ=90
Wykaż, że α+β+γ=90 



 https://matematykaszkolna.pl/forum/246976.html ?
https://matematykaszkolna.pl/forum/246976.html ?