dzielenie wielomianów wielomian: czy jest jakiś inny sposób dzielenia oprócz pisemnego ? Jeśli tak to który sposób lepiej stosować. Umiem tylko pisemnie.

Draghan: Masz łatwy w zastosowaniu schemat Hornera, ale tylko jeśli dzielisz przez dwumian https://matematykaszkolna.pl/strona/1401.html

5-latek: I dobrze ze pisemnie umiesz Horner nie wybacza bledu −niestety

Hajtowy: Nie wybacza ale jest prostszy i szybszy

Draghan: Witaj, 50latek Żadne rachunki błędu nie wybaczają A dzielenie pisemne jest mocno błędo−płodne Przynajmniej w moim wydaniu wielomian, ciesz się, że umiesz to dzielenie Jak ja zdawałem maturę, to jakoś nie za bardzo umiałem

Draghan: 5−latek *

5-latek: czesc Darghan Co do wczorajszsego postu tak to jest polówka kąta .

Draghan: Zrobiłem z Ciebie pięćdziesięciolatka Ale to nieumyślnie, przepraszam O, dzięki Wzór sobie spisałem, żeby się nie zgubił

5-latek: Nic nie szkodzi Nawet mi ujales lat . czuje sie przez to mlodszy

Draghan: To na powrót bądź 5−latek Jeszcze lepiej, prawda?

5-latek: Pewnie ze tak . jak znajde jeszce jaies przydatne wzory to CI napiszse

Draghan: Na pewno nie zaszkodzi Dzięki

Piotr 10: Twierdzenie Ptolemeusza polecam

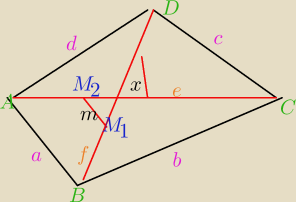
5-latek: czworokat wypukly A B C D −−katy czworokata a b c d − boki czworokata M₁ i M₂ srodki przekatnych e i f to przekatne m=M₁M₂ x− kat miedzy przekatmymi A+B+C+D=360 stopni 1.a²+b²+c²+d²= e²+f²+4m²

	1		1
S=		absinB+		cdsinD
	2		2

W rownolegloboku a=c b=d m=0 e²+f²=2(a²+b²) S=ab*sinB

	1
2. S=		e*f*sinx
	2

3. e²*f²= a²c²+b²d²−2abcd cos2w(uwaga przez w oznaczylem male omega ) gdzie 2w=A+C lub B+D Jezeli czworokat jest wpisany w kolo to 2w=180 stopni e*f=ac+bd(Twierdzenie Ptomeleusza

	a+b+c+d		A+C		B+D
S=√(p−a)(p−b)(p−c)(p−d)−2abcd*cos2w gdzie p=		w=		lub w=
	2		2		2

Draghan: Jeszcze muszę przetrawić, co tutaj zostało ciekawego zawarte, ale już zasłużyłeś na , choćby za samo napisanie tego

Trivial: Odnośnie dzielenia wielomianów sposobem tradycyjnym to warto zauważyć, że nie trzeba pisać tych wszystkich x³, x², x⁵, itd... Można to opuścić jeśli będzie się konsekwentnie zapisywać wszystko w kolumnach. Przykładowo:

	x5 + 3x4 − 2x3 + x − 1
		= ?
	x2+1

1 3 −3 −3 1 3 −2 0 1 −1 : 1 0 1 − 1 0 1 3 −3 0 − 3 0 3 −3 −3 1 + 3 0 3 −3 4 −1 + 3 0 3 4 2 Zatem:

	x5 + 3x4 − 2x3 + x − 1		4x+2
		= x3 + 3x2 − 3x − 3 +		.
	x2+1		x2+1

Nie ma tyle hałasu o nic w zapisie...

Draghan: Heh Prawie jak w dwójkowym Ja wolę jednak chyba stare, sprawdzone przepisywanie iksów. Przynajmniej wiem, na co patrzę A mam talent do opuszczania niektórych wyrazów, np. przy mnożeniu i dzieleniu dłuższych wyrażeń, także spisywanie wszystkiego jest dla mnie bezpieczniejsze Może już czas na okulary?

Trivial: Co jest bezpiecznego w przepisywaniu cały czas tego samego? Jak dla mnie to każde powtarzanie prowadzi do błędów wcześniej czy później. Po wywaleniu wszelkich iksów takie dzielenie przypomina normalnie dzielenie pisemne (bez pożyczek).

5-latek: Draghan . W twoim wieku okulary Ty jeszce nie musisz przejrzec na oczy

Draghan: Tak pomyślałem, jak jest wyżej napisane Może jak poćwiczę bez tego przepisywania, będzie rzeczywiście łatwiej I długopis się oszczędza

Draghan: 5−latek − skąd wiesz, ile to jest w moim przypadku "w twoim wieku"?

Trivial: Draghan, 20 lat?

5-latek: No 20 lat bo pisales ze w tamtym roku nie poszla CI matura z matematyki czy dobrze wywnioskowalem ?

Draghan: Poszła maturka, poszła Jak na trzy miesiące uczenia się matematyki rozszerzonej, to nawet poszła przyzwoicie Zagadka rozwiązana poprawnie, chociaż rocznikowo mam 21 (jestem z grudnia) Bo technikum jest czteroletnie