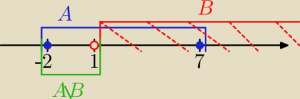
Różnica zbiorów proszeopomoc: Jeśli A = <−2,7>, B= (1, +∞), to wówczas A\B jest przedziałem:.

Marcin: Próbowałeś sobie to zobrazować rysunkiem? Bardzo pomaga.

Dziadek Mróz:

Eta: Echhh kto się ukrywa pod tym nickiem ?

Marcin: Może Eta?

Eta: ... ale ktoś mi znany ... tylko kto?

bezendu: Mila

Eta: Pewnie tak

Eta: A jednak nie ... bo Mila jest też na forum

Marcin: Jak ktoś znany, na pewno Mila

Marcin: wiem! Jakub!

Dziadek Mróz: Eee nikt znany, ale sposób jest podchwycony od kogoś

ZKS: Sposób który pokazywał Bogdan.

Dziadek Mróz: O dokładnie, a o mnie zapomnijcie, jestem nikim ważnym Nawet nie jestem matematykiem

proszeopomoc: Myślałem, że wiem co to jest różnica zbiorów, tylko w odpowiedziach ja bym zaznaczył <−2,1>, a prawidłową odpowiedzią podobno jest <−2,1). Przecież jedynka nie należy do zbioru B, a należy do zbioru A, więc czego tu nie rozumiem?

Mila: Hej, witam Was, zobaczcie tam, nie mogę się zorientować co Pigor ma na myśli? https://matematykaszkolna.pl/forum/246901.html

pigor: ..., przepraszam Mila , to mi czas odpocząć ... dobranoc

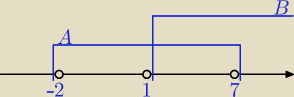
Bogdan: Mój rysunek wygląda tak. Ja nie zamalowuję kółeczek i nie rysuję pod osią. Jeśli A\B to wyobrażamy sobie, że wymazujemy B.

Piotr: a ja wtrace swoje 3 grosze (przynajac, ze rysunki Bogdana sa znakomite) moze ktos woli tak : A\B − wszystko co jest w A a nie ma w B.

proszeopomoc: czyli <−2, 1)

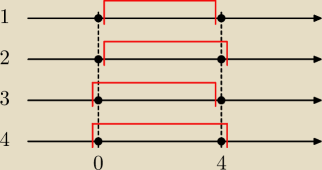
Dziadek Mróz: Interpretacja rysunków: 1. (0, 4) 2. (0, 4> 3. <0, 4) 4. <0, 4> Gdy liczba zakresu jest nieostra "(, )" to linię zakresu rysujemy od wewnątrz zakresu nie obejmując tej liczby. Gdy liczba zakresu jest ostra "<, >" to linię zakresu rysujemy od zewnątrz zakresu obejmując tą liczbę. Sposób Bogdana jest znakomity i prosty w obsłudze, podczas obcinania, szukania części wspólnej widać jak na dłoni, które liczby należą do zakresu a które nie.