zadanie z geometrii analitycznej Dawidz: Wyznacz rownanie okregu, ktory otrzymamy po przeksztalceniu okregu (x−4)² + (y+6)² = 36 w symetrii wzgledem punktu O=(−3,5) i w jednokladnosci o skali k=−²₃ . Na stronie jest rozwiazanie tego zadania ale nie zabardzo rozumiem skad sie tam wszystko wzielo, dlatego pytam ponownie. Odpowiedz ktora ma wyjsc: (x+²³₃)²+(y−³⁷₃)²=16 (rozumiem ze r=6 i 6*²₃ = 4, stad r²=16)

alo: Środek okręgu S=(4;−6) i na wektorach:

2
	OS=OS`
3

Dawidz: O tym to ja wiem alo, problem polega na tym ze nie wychodzi mi to, co ma wyjsc... prawdopodobnie nie potrafie liczyc bo robie to tak: S=(4,−6) S'=(x,y) O=(−3,5) |OS`|=−²₃|OS| [x+3,y−5]=−²₃[−3−4,−6−5] x+3=−²₃(−7) x+3=¹⁴₃ x=¹⁴₃−⁹₃ x=⁵₃ dla y nie bede robil bo tez wychodza glupoty...

alo: Odwrotnie robisz OS

alo: Przepraszam, źle spojrzałem. k=2/3. minus świadczy tylko o tym gdzie znajduje się punkt O

Dawidz: no wlasnie, teraz zauwazylem ze jesli zamiast −7 byloby 7 to wynik wyszedlby dobry, bo x+3=−²₃(7) x+3=−¹⁴₃ x=−¹⁴₃−⁹₃ x=−²³₃ no ale wzor to powinno byc chyba cos takiego [x₁−x₂, y₁−y₂]?

Dawidz: dobra zignoruj moja wczesniejsza wypowiedz, nie zauwayzlem tego co dopisales wyzej. Czyli rozumiem, ze minusa trzeba wszedzie "olac", wiec z tego co widze to jest on w tym zadaniu calkowicie zbedny, jesli O mamy podane? "minus świadczy tylko o tym gdzie znajduje się punkt O"

Dawidz: To teraz ze tak zapytam − gdzie znajdowal by sie punkt O jesli k=²₃ a nie k=−²₃?

alo: 902 Tu jest dobrze wyjaśnione.

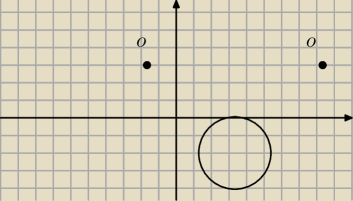
Dawidz: Wielkie dzieki, nie ma tam niestety jednokladnosci wzgledem okreslonego punktu, ale z tego co zauwazylem to minus wplynalby na to, ze punkt O bylby po prawo od punktu S a nie na lewo? sorry za beznadziejny rysunek ale mam nadzieje ze widac o co chodzi.

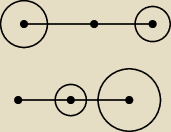
alo: 1 rysunek to k<0 SO`=<sup>2</sup><sub>3</sub>OS (swoja droga znowu chochlik w pierwszym poscie) 2 k>0 OS`=²₃OS Jeżeli jednokładność jest dodatnia to S₁ i S₂ leżą po tej samej stronie punktu O Jeżeli ujemna to są po różnych stronach

Dawidz: Ok, dzieki za pomoc