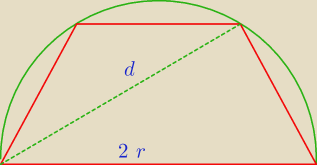
Planimetria bezendu: W półkole o promieniu r wpisano trapez równoramienny o przekątnej długości d . Oblicz długość krótszej podstawy trapezu Coś na kątach ?

Saizou: jest to trapez rownoramienny i trojkat prostokatny, oraz ramie + warunek wpisania czworokata

Mila: Kąt wpisany oparty na średnicy...

Godzio: Mój pomysł (na szybko więc pewnie jest prostszy sposób) Wylicz z Pitagorasa c (dlaczego tam jest kąt prosty) ? Z twierdzenia sinusów albo cosinusów policz odpowiednio sinus albo cosinus α. Skorzystaj z tego, że α + β = 180^o

bezendu: Przekątna zawiera się w dwusiecznej ? Jak tam jest kąt prosty to mogę obliczyć c z tw sinusów i potem a również z tw sinusów ?

bezendu: albo z twierdzenia o średniej geometrycznej ?

Mila: c²=4r²−d² a=2r

	a+b		a−b
h2=		*		srednia geometryczna
	2		2

	a−b
h2=c2−(		)2 Pitagoras.
	2

porównaj

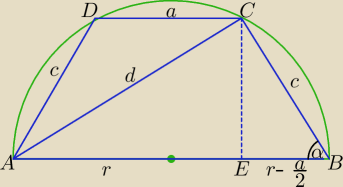
Bogdan: c² = 4r² − d²

	c		a   r −   2
ΔABC ∼ ΔEBC ⇒		=		⇒ c2 = 2r2 − ar
	2r		c

	d2 − 2r2
4r2 − d2 = 2r2 − ar ⇒ a =
	r

Bogdan: albo

	a   r +   2		d		d2 − 2r
ΔAED ∼ ΔABC ⇒		=		⇒ 2r2 + ar = d2 ⇒ a =
	d		2r		r

bezendu: Dziękuję.

zawodus: Bezendu a gdzie twój post choćby z linijką własnego pomysłu?

bezendu: 00:07

zawodus: Tylko trochę rachunków mi brakuje

bezendu: Ja pytałem tylko o sposób. Czy z tej metody nie prosiłem wcale o rozwiązanie.

bezendu: i właśnie czy tam jest kąt prosty czy go nie ma ?

zawodus: Jest kąt prosty.

bezendu: ale czemu tam jest 90⁰ ?

Draghan: Ponieważ trójkąt opiera się na średnicy okręgu Jeśli pytasz o to, co myślę

Draghan: W sensie że kąt się opiera A jeden z boków trójkąta jest właśnie tą średnicą

Marcin: https://matematykaszkolna.pl/strona/465.html Tak jak mówi Draghan

zawodus: Trójkąt się opiera? A kto go kusi, że musi się opierać?

Draghan: Środkowa go kusi, żeby poszedł na połówkę

5-latek: Albo do Ety na π− kę