 Dane jest równanie x2 + (2−3m)x + 2m2 − 5m− 3=0
a) Wyraź iloczyn pierwiastków tego równania jako funkcję zmiennej m i oznacz ją f(m). Określ
dziedzinę tej funkcji.
b) Dla jakich wartości m funkcja f(m) osiąga minimum.
c) Wyznacz pierwiastki równania tak by ich iloczyn był najmniejszy.
Dane jest równanie x2 + (2−3m)x + 2m2 − 5m− 3=0
a) Wyraź iloczyn pierwiastków tego równania jako funkcję zmiennej m i oznacz ją f(m). Określ
dziedzinę tej funkcji.
b) Dla jakich wartości m funkcja f(m) osiąga minimum.
c) Wyznacz pierwiastki równania tak by ich iloczyn był najmniejszy.
 zapomniałam o wzorach.
zapomniałam o wzorach.
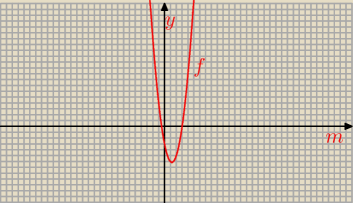 a)
a)
| c | ||
y = f(m) = | = 2 m2 − 5 m − 3 | |
| a |
| 5 | 5 | |||
m = p = | = | |||
| 2*2 | 4 |
| 5 | ||
Dla m = | mamy równanie: | |
| 4 |
| 7 | 49 | |||
x2 − | x − | = 0 | ||
| 4 | 8 |
| 7 | 7 | |||
x1 = − | , x2 = | |||
| 4 | 2 |
| 5 | ||
czy w przykładzie b) nie musze podstawić | w miejsce m i wyliczyć tę wartosc? | |
| 4 |